

分析 (1)如图①中,分别以A、B为圆心AB长为半径画弧,两弧交于点E,△ABE即为等边三角形;
(2)如图②中,在BC上取一点H,使得AB=BH,作△ABH的外接圆交AD于M,则当点F在$\widehat{MH}$上时,∠AFB=∠AHB=45°,当F是$\widehat{MH}$的中点时,△ABF的面积最大;
(3)如图③中,在BC上取一点E,使得∠AEB=30°,在AD上取一点F,使得∠CFD=30°,连接AC,分别作△ABE,△DFC的外接圆交AC于M、N.此时△ABM≌△CDN,且面积最大;
解答 解:(1)如图①中,分别以A、B为圆心AB长为半径画弧,两弧交于点E,△ABE即为等边三角形.
S△ABE=$\frac{\sqrt{3}}{4}$•32=$\frac{9\sqrt{3}}{4}$.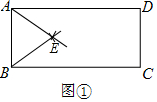
(2)如图②中,在BC上取一点H,使得AB=BH,作△ABH的外接圆交AD于M,则当点F在$\widehat{MH}$上时,∠AFB=∠AHB=45°,
当F是$\widehat{MH}$的中点时,△ABF的面积最大,最大面积=$\frac{1}{2}$•3•($\frac{3}{2}$+$\frac{3\sqrt{2}}{2}$)=$\frac{9+9\sqrt{2}}{4}$.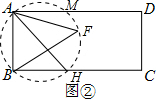
(3)如图③中,在BC上取一点E,使得∠AEB=30°,在AD上取一点F,使得∠CFD=30°,连接AC,
分别作△ABE,△DFC的外接圆交AC于M、N.此时△ABM≌△CDN,且面积最大,连接EM.
∵AE是直径,
∠AME=∠EMC=90°,∵∠ECM=∠ACB,
∴△ECM∽△ACB,
∴EC:AC=CM:BC,
∵AC=$\sqrt{{3}^{2}+(2\sqrt{10})^{2}}$=7,EC=2$\sqrt{10}$-3$\sqrt{3}$,
∴(2$\sqrt{10}$-3$\sqrt{3}$):7=CM:2$\sqrt{10}$,
∴CM=$\frac{40-6\sqrt{30}}{7}$,AM=7-CM=$\frac{9+6\sqrt{10}}{7}$,
∴S△ABM:S△ABC=AM:AC,
∴S△ABM=$\frac{27\sqrt{10}+180}{49}$.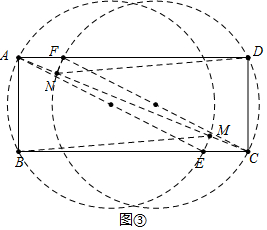
点评 本题考查四边形综合题、矩形的性质、等边三角形的判定和性质、圆周角定理、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加辅助圆解决问题,属于中考压轴题.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC在网格中(每格表示1个单位),如图所示构建平面直角坐标系
如图,△ABC在网格中(每格表示1个单位),如图所示构建平面直角坐标系查看答案和解析>>
科目:初中数学 来源: 题型:解答题
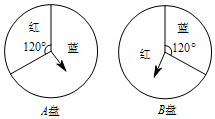 小明和小丽用如图所示的两个转盘做“配紫色”游戏:分别转动两个转盘,其中一个转盘转到红色,另一个转盘转到蓝色,即可配成紫色,两人商定,若能配成紫色,小明胜,否则小丽胜,这个游戏对双方公平吗?请说明理由.
小明和小丽用如图所示的两个转盘做“配紫色”游戏:分别转动两个转盘,其中一个转盘转到红色,另一个转盘转到蓝色,即可配成紫色,两人商定,若能配成紫色,小明胜,否则小丽胜,这个游戏对双方公平吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
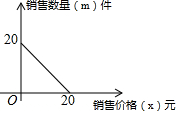 某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图象如图所示.
某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )
如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | (1,-1) | C. | ($\frac{1}{2}$,-$\frac{1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,下列说法:
“龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com