

分析 (1)根据观察,可发现规律这样的三角形有n个时,则需要火柴棒2n+1跟,根据规律,可得答案;
(2)根据观察,可发现规律这样的三角形有n个时,则需要火柴棒2n+1跟,根据规律,可得答案;
(3)根据观察,可发现规律这样的三角形有n个时,则需要火柴棒2n+1跟,根据规律,可得答案.
解答 解:观察:第一个是2+1,
第二个是2×2+1,
第三个是2×3+1,
(1)若这样的三角形有6个时,则需要火柴棒2×6+1=13根
(2)若这样的三角形有n个时,则需要火柴棒2n+1跟;
(3)设可组成n个三角形,由题意,得
2n+1=1001,
解得n=500,
故答案为:13,2n+1,500.
点评 本题考查了规律性,观察发现规律是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
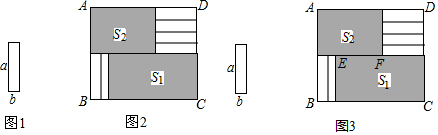
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
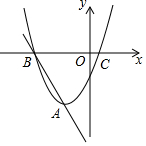 已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.
已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在只装了红球的袋子中摸到白球 | |
| B. | 某射击运动员射击一次,命中靶心 | |
| C. | 任意画一个三角形,其内角和是180° | |
| D. | 掷一枚质地均匀的正方体骰子,向上的一面点数是3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com