
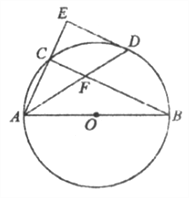
【题目】如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
(1)求证:∠BAD=∠DAE;
(2)若AB=6,AD=5,求DF的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)连接OD,由ED为⊙O的切线,根据切线的性质得到OD⊥ED,由AB为⊙O的直径,得到∠ACB=90°,根据平行线的判定和性质得到角之间的关系,又因为OA=OD,得到∠BAD=∠ADO,推出结论∠BAD=∠DAE;
(2)连接BD,得到∠ADB=90°,由勾股定理得到![]() ,根据三角函数的定义得到tan∠CBD=tan∠BAD=
,根据三角函数的定义得到tan∠CBD=tan∠BAD=![]() ,由DF=BDtan∠CBD=
,由DF=BDtan∠CBD=![]() .
.
详解:(1)连接OD,
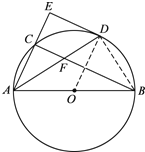
∵ED为⊙O的切线,
∴OD⊥ED,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC∥ED,
∴∠ACB=∠E=∠EDO,
∴AE∥OD,
∴∠DAE=∠ADO,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠BAD=∠DAE;
(2)连接BD,
∴∠ADB=90°,
∵AB=6,AD=5,
∴![]() ,
,
∵∠BAD=∠DAE=∠CBD,
∴tan∠CBD=tan∠BAD=![]() ,
,
在Rt△BDF中,
∴DF=BDtan∠CBD=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在长和宽分别是a,b的长方形的四个角都剪去一个边长为x的正方形,折叠后,做成一无盖的盒子(单位:cm).
(1)用a,b,x表示纸片剩余部分的面积;
(2)用a,b,x表示盒子的体积;
(3)当a=10,b=8且剪去的每一个小正方形的面积等于4 cm2时,求剪去的每一个正方形的边长及所做成的盒子的体积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
如图,已知女排球场的长度OD为18米,位于球场中线处的球网AB的高度为2.24米,一队员站在点O处发球,排球从点O的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为6米时,到达最高点F,以O为原点建立如图所示的平面直角坐标系.
(1)当排球运行的最大高度为2.8米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)之间的函数关系式.
(2)在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由.
(3)喜欢打排球的李明同学经研究后发现,发球要想过网,球运行的最大高度h(米)应满足h>2.32,但是他不知道如何确定h的取值范围,使排球不会出界(排球压线属于没出界),请你帮忙解决并指出使球既能过网又不会出界的h的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
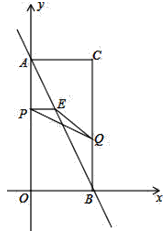
【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,移动电商发展迅速,以下是2017年某调查机构发布的相关的统计表和统计图的一部分。请根据以上信息解答下列问题:
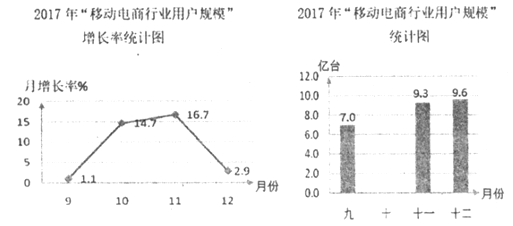
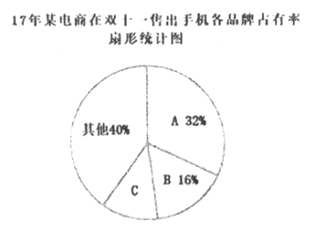
(1)2017年10月“移动电商行业用户规模”是___________亿台(结果精确到0.1亿台);并补全条形统计图;
(2)2017年10—12这三个月“移动电商行业用户规模”比上个月增长台数的平均数为___________亿台,若按此平均数增长,请你估计2018年1月“移动电商行业用户规模”为___________亿台(结果精确到0.1亿台);
(3)2017年某电商在双十一共售出手机12000台,则C品牌手机售出的台数是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到![]() ,第2次移动到
,第2次移动到![]() ,第3次移动到
,第3次移动到![]() ,……,第n次移动到
,……,第n次移动到![]() ,则△O
,则△O![]() 的面积是( )
的面积是( )

A.504B.![]() C.
C.![]() D.505
D.505
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点![]() 、
、![]() 、
、![]() 、
、![]() 对应的数分别是
对应的数分别是![]() ,且
,且![]() .
.
(1)那么![]() ,
,![]() :
:
(2)点![]() 以
以![]() 个单位/秒的速度沿着数轴的正方向运动,
个单位/秒的速度沿着数轴的正方向运动,![]() 秒后点
秒后点![]() 以
以![]() 个单位/秒的速度也沿着数轴的正方向运动,当点
个单位/秒的速度也沿着数轴的正方向运动,当点![]() 到达点
到达点![]() 处立刻返回,与点
处立刻返回,与点![]() 在数轴的某点处相遇,求这个点对应的数;
在数轴的某点处相遇,求这个点对应的数;
(3)如果![]() 、
、![]() 两点以(2)中的速度同时向数轴的负方向运动,点
两点以(2)中的速度同时向数轴的负方向运动,点![]() 从图上的位置出发也向数轴的负方向运动,且始终保持
从图上的位置出发也向数轴的负方向运动,且始终保持![]() ,当点
,当点![]() 运动到
运动到![]() 时,点
时,点![]() 对应的数是多少?
对应的数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的长为6,宽为4,将长方形先向上平移2个单位,再向右平移2个单位得到长方形![]() ,则阴影部分面积是( )
,则阴影部分面积是( )
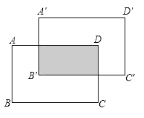
A.12B.10C.8D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
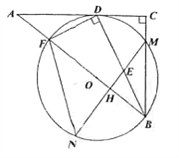
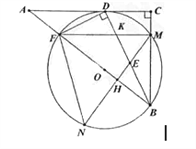
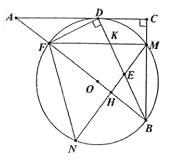
【题目】如图,在Rt△ABC中,∠C=90°,D为AC上一点,连接BD,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相较于点M,与AC相切于点D。过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.
(1)求证:BD平分∠ABC;
(2)连接FM与BD相交于点K,求证:MK=ME;
(3)若AF=1,tan∠N=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com