
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 .
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 . 
【答案】40
【解析】解:过点A作AM⊥x轴于点M,如图所示. 设OA=a,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB= ![]() ,
,
∴AM=OAsin∠AOB= ![]() a,OM=
a,OM= ![]() =
= ![]() a,
a,
∴点A的坐标为( ![]() a,
a, ![]() a).
a).
∵点A在反比例函数y= ![]() 的图象上,
的图象上,
∴ ![]() a×
a× ![]() a=
a= ![]() a2=48,
a2=48,
解得:a=10,或a=﹣10(舍去).
∴AM=8,OM=6,OB=OA=10.
∵四边形OACB是菱形,点F在边BC上,
∴S△AOF= ![]() S菱形OBCA=
S菱形OBCA= ![]() OBAM=40.
OBAM=40.
故答案是:40.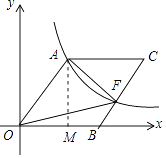
过点A作AM⊥x轴于点M,设OA=a,通过解直角三角形找出点A的坐标,结合反比例函数图象上点的坐标特征即可求出a的值,再根据四边形OACB是菱形、点F在边BC上,即可得出S△AOF= ![]() S菱形OBCA , 结合菱形的面积公式即可得出结论.
S菱形OBCA , 结合菱形的面积公式即可得出结论.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某校组织同学到离校15千米的社会实践基地开展活动.一部分同学骑自行车前往,另一部分同学在骑自行车的同学出发 ![]() 小时后,乘汽车沿相同路线行进,结果骑自行车的与乘汽车的同学同时到达目的地.已知汽车速度是自行车速度的3倍,求自行车的速度.
小时后,乘汽车沿相同路线行进,结果骑自行车的与乘汽车的同学同时到达目的地.已知汽车速度是自行车速度的3倍,求自行车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”.例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)已知点A(﹣2,6)的“![]() 级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;
级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;
(2)已知点M(m﹣1,2m)的“﹣3级关联点”M′位于y轴上,求M′的坐标;
(3)已知点C(﹣1,3),D(4,3),点N(x,y)和它的“n级关联点”N′都位于线段CD上,请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D. 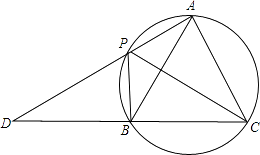
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2 ![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是 . (写出正确命题的序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(﹣1,m)和点B(n,5). 
(1)求该二次函数的关系式;
(2)在给定的平面直角坐标系中,画出这两个函数的大致图象;
(3)结合图象直接写出x2+bx+c>x+1时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE. 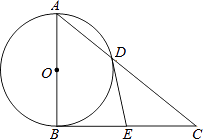
(1)求证:DE与⊙O相切.
(2)若tanC= ![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com