练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
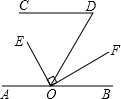
    20．已知：AB∥CD，OE平分∠AOD，OF⊥OE于O，∠D=60°，则∠BOF=30°．

    分析 根据平行线的性质和直角、角平分线的定义求解．

    解答 解：∵AB∥CD，
    ∴∠AOD=180°-∠D=180°-60°=120°，∠BOD=∠D=60°．
    ∵OE平分∠AOD，
    ∴∠EOD=120°÷2=60°．
    ∵OF⊥OE，
    ∴∠DOF=90°-60°=30°，
    ∴∠BOF=∠BOD-∠DOF=60°-30°=30°．
    故答案为：30°．

    点评 此题主要考查平行线的性质：两直线平行，同旁内角互补；两直线平行，内错角相等．综合利用了直角、角平分线的定义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．如图，抛物线y=-（x-1）2+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（-1，0）．
    （1）求点B，C的坐标．
    （2）判断△CDB的形状并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

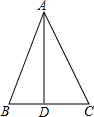    11．如图，△ABC中，∠BAC=45°，AD⊥BC于D，BD=2，AD=6，求CD的长，小明同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题．请按照小明的思路，探究并解答下列问题：
    （1）分别以AB、AC为对称轴，画出△ABD和△ACD的轴对称图形，D点的对称点分别为E、F，延长EB，FC交于M点，判断四边形AEMF的形状，并说明理由；
    （2）设CD=x，利用勾股定理，在△BCM中建立关于x的方程模型，并求出x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．△DEF是由△ABC平移得到的，点A（-2，-1）的对应点为D（1，-3），则点C （2，3）的对应点F的坐标为（　　）
    A．（-1，5）B．（1，5）C．（5，1）D．（5，-4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知2是x的立方根，且（y-2z+5）2+$\sqrt{z-3}$=0，求$\root{3}{x+{y}^{3}+{z}^{3}-9}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知AB∥CD，分别探讨四个图形中∠APC，∠A，∠C的关系．

    （1）请说明图1，图2中三个角的关系，并任选一个说明理由．
    （2）猜想图3，图4中三个角的关系，不必说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

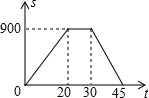    12．乐平街上新开张了一家“好又多”超市，这个星期天，张明和妈妈去这家新开张的超市买东西，如图反映了张明从家到超市的时间t（分钟）与距离s（米）之间关系的一幅图．
    （1）图中反映了哪两个变量之间的关系？超市离家多远？
    （2）张明从家出发到达超市用了多少时间？从超市返回家花了多少时间？
    （3）张明从家出发后20分钟到30分钟内可能在做什么？
    （4）张明从家到超市时的平均速度是多少？返回时的平均速度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如对于任意的实数a、b都有f（a+b）=f（a）+f（b）且f（1）=2，则$\frac{f（2）}{f（1）}$+$\frac{f（4）}{f（2）}$+$\frac{f（6）}{f（3）}$+…+$\frac{f（2012）}{f（1006）}$的值是（　　）
    A．1005B．1006C．2012D．2010

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图一，平行四边形ABCD，点M为AD的中点，过D点任意作一直线分别交BM、BC的延长线于E、F点，AF与BE交于N点．
    （1）若CF=$\frac{1}{4}$BC，则$\frac{MD}{BF}$的值为$\frac{2}{5}$，$\frac{DE}{DF}$的值为$\frac{2}{3}$；
    （2）求证：MN•EB=BN•ME；
    （3）如图二，平行四边形ABCD中，若AB⊥BC，证明：∠EAD=∠FAD．

    查看答案和解析>>

    同步练习册答案