
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:AC•AD=AB•AE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.


【考点】切线的性质;相似三角形的判定与性质.
【分析】(1)连接DE,根据圆周角定理求得∠ADE=90°,得出∠ADE=∠ABC,进而证得△ADE∽△ABC,根据相似三角形对应边成比例即可求得结论;
(2)连接OD,根据切线的性质求得OD⊥BD,在RT△OBD中,根据已知求得∠OBD=30°,进而求得∠BAC=30°,根据30°的直角三角形的性质即可求得AC的长.
【解答】(1)证明:连接DE,
∵AE是直径,
∴∠ADE=90°,
∴∠ADE=∠ABC,
∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴
 =
=
 ,
,
∴AC•AD=AB•AE;
(2)解:连接OD,
∵BD是⊙O的切线,
∴OD⊥BD,
在RT△OBD中,OE=BE=OD,
∴OB=2OD,
∴∠OBD=30°,
同理∠BAC=30°,
在RT△ABC中,AC=2BC=2×2=4.


【点评】本题考查了圆周角定理的应用,三角形相似的判定和性质,切线的性质,30°的直角三角形的性质等,作出辅助线构建直角三角形是解题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源:2015年初中毕业升学考试(新疆生产建设兵团卷)数学(解析版) 题型:选择题
(5分)如图所示,某同学的家在A处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )

A.A→C→D→B B.A→C→F→B
C.A→C→E→F→B D.A→C→M→B
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线AB∥CD,BE平分∠ABC,交CD于点D, ∠CDB=30°,那么∠C的度数为( )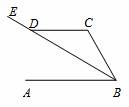
A.150° B.130° C.120° D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点.当a ≤ x ≤ b时,有-1 ≤ y1 - y2 ≤ 1成立,则称这两个函数在a ≤ x ≤ b上是“相邻函数”,否则称它们在a ≤ x ≤ b上是“非相邻函数”.例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1- y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2并研究它在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
(1)判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,并说明理由;
(2)若函数y = x2- x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;
(3)若函数y = 与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值.
与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
小明投资销售一种进价为每件20元的护眼台灯.销售 过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.(3分)
(2)当销售单价定为多少元时,每月可获最大利润?每月最大利润是多少?(2分)
(3)如 果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)(3分)
果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com