
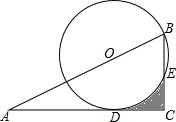
 在Rt△ABC中,∠C=90°,∠A=30°,O在斜边AB上,半径为4cm的圆O过点B,切AC于点D,交BC于点E.
在Rt△ABC中,∠C=90°,∠A=30°,O在斜边AB上,半径为4cm的圆O过点B,切AC于点D,交BC于点E.分析 (1)如图1所示:连接OE、OD.由切线的性质可知OD⊥AD,依据含30°直角三角形的性质可求得OA的长,从而可求得AB的长,然后在三角形ABC中依据含30°直角三角形的性质可求得BC的长,接下来,证明△OBE为等边三角形,从而可求得BE的长,依据EC=BC-BE可求得EC的长;
(2)如图2所示:连接OD、OE,过点E作EF⊥OD,垂足为F.在Rt△OEF中,先求得EF的长度,然后依据S阴=S梯形ECDO-S扇形EOD求解即可.
解答 解:(1)如图1所示:连接OE、OD.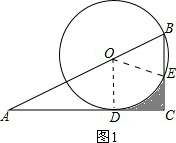
∵AC圆O相切,D为切点,
∴OD⊥AD.
∵在Rt△AOD中,∠A=30°,OD=4,
∴OA=8.
∴AB=8+4=12.
∵在Rt△ABC中,∠A=30°,AB=12,
∴BC=6.
∵∠A=30°,∠C=90°,
∴∠B=60°.
又∵OB=OE,
∴△OBE为等边三角形.
∴BE=OE=0B=4.
∴EC=BC-BE=6-4=2.
(2)如图2所示:连接OD、OE,过点E作EF⊥OD,垂足为F.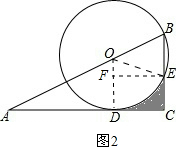
∵OD⊥AC,BC⊥AC,
∴OD∥BC.
∴∠B+∠BOD=120°.
∴∠BOD=120°.
∵△OBE为等边三角形,
∴∠BOE=60°.
∴∠EOF=60°.
在Rt△OEF中,EF=$\frac{\sqrt{3}}{2}$OE=2$\sqrt{3}$.
∴S阴=S梯形ECDO-S扇形EOD=$\frac{(2+4)×2\sqrt{3}}{2}$-$\frac{60π×{4}^{2}}{360}$=6$\sqrt{3}$-$\frac{8π}{3}$.
点评 本题主要考查的是切线的性质、垂径定理、等边三角形的性质和判定、勾股定理的应用以及不规则图形的面积计算方法,掌握本题的辅助线的作法是解题的关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 某书稿中的错别字 | B. | 调查七(1)班学生的身高情况 | ||
| C. | 某品牌灯泡的使用寿命 | D. | 企业招聘,对应聘人员进行面试 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com