
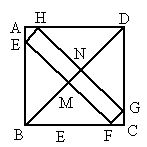
如图所示,已知正方形ABCD的对角线长为a,四边形EFGH的四个顶点E、F、G、H分别在AB、BC、CD、DA上滑动,在滑动过程中,始终有EH∥BD∥FG,且EH=FG,那么四边形EFGH的周长是否可求?若能求出,它的周长是多少?若不能求出,请说明理由.
|
解:能求出四边形 EFGH的周长.由EH∥BD∥FG,EH=FG ,得四边形EFGH是平行四边形,所以 EF∥GH,得四边形EMNH、四边形MNFD都是平行四边形,所以 EH=GF=MN,而∠AEH=∠ABD=45°,∠AHE=∠ADB=45°,同理∠ CFG=∠CGF=45°,所以△AEH和△CGF关于BD轴对称,所以 AFH和△CGF关于GN=MF=NH=EM,AH=CG.又因为 AD=CD,所以DH=DG又因为∠HDN=∠GDN=45°,所以∠ DHN=∠DGN=45°,故HN=DN.同理 EM=MF=BM,GN=HN=DN,所以 EF+FG+GH+HE=2(BM+MN+ND)=2BD=2a. |
|
这是近几年中考出现的动点问题,也是一个开放性题目,先假设能求出周长,想办法把所求的周长同已知的对角线的长联系起来. 关键是转移相等线段,利用正方形和平行四边形、等腰三角形的特征. |


科目:初中数学 来源: 题型:
 30、如图所示,已知正方形ABCD,E为BC上任意一点,延长AB至F,使BF=BE,AE的延长线交CF于G,
30、如图所示,已知正方形ABCD,E为BC上任意一点,延长AB至F,使BF=BE,AE的延长线交CF于G,查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知正方形ABCD的面积是8平方厘米,正方形EFGH的面积是62平方厘米,BC落在EH上,△ACG的面积是4.9平方厘米,则△ABE的面积是( )
如图所示,已知正方形ABCD的面积是8平方厘米,正方形EFGH的面积是62平方厘米,BC落在EH上,△ACG的面积是4.9平方厘米,则△ABE的面积是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知正方形OABC的面积为9,点B在函数y=
如图所示,已知正方形OABC的面积为9,点B在函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com