
【题目】已知关于x的一元二次方程x2﹣(m+2)x+2m=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若直角△ABC的两直角边AB、AC的长是该方程的两个实数根,斜边BC的长为3,求m的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
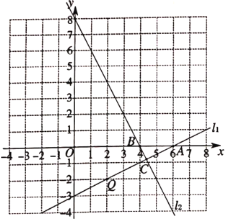
【题目】如图,直线![]() 经过点
经过点![]() ,与x轴交于点
,与x轴交于点![]() ,直线
,直线![]() 与x轴相交于点B,与直线
与x轴相交于点B,与直线![]() 相交于点C.
相交于点C.
(1)求直线![]() 的表达式;
的表达式;
(2)M的坐标为![]() ,当
,当![]() 取最小时.
取最小时.
①求M点坐标;
②横,纵坐标都是整数的点叫做整点.直接写出线段AM、BM、BC、AC围成区域内(不包括边界)整点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货价为30元的书包以40元售出,平均每月能售出600个,调查表明:这种书包的售价每上涨1元,其销售量就减少10个.
(1)为了使平均每月有10000元的销售利润,这种书包的售价应定为多少元?
(2)10000元的利润是否为最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时书包的售价为多少元?
(3)请分析并回答售价在什么范围内商家就可以获得利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的盒子中,分别装有除颜色外其它均相同的小球,其中,甲盒子装有2个白球,1个红球:乙盒子装有2个红球,1个白球.
(1)将甲盒子摇匀后,随机取出一个小球是红球的概率是______;
(2)小华和小明商定:将两个盒子摇匀后,各随机摸出一个小球.若颜色相同,则小华获胜;若颜色不同,则小明获胜,请用列表法或画出树状图的方法说明谁贏的可能性大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B,与y轴的正半轴交于点C.现有下列结论:①abc>0;②4a﹣2b+c>0;③2a﹣b>0;④3a+c=0,其中,正确结论的个数是( )
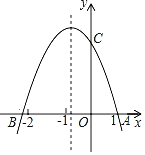
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
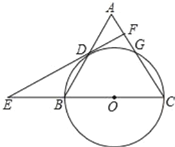
【题目】如图,在![]() ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
①DF⊥AC; ②DO=DB; ③S△ABC=48; ④cos∠E=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1)和B(x2,y2)均在二次函数y=ax2﹣6ax+9a﹣4的图象上,且|x1﹣3|<|x2﹣3|,则下列说法错误的是( )
A.直线x=3是该二次函数图象的对称轴
B.当a<0时,该二次函数有最大值﹣4
C.该二次函数图象与坐标轴一定有一个或三个交点
D.当a>0时,y1<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
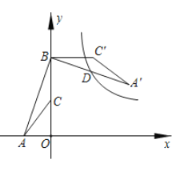
【题目】如图,点A(-2,0), 点B(0,6),C为OB的中点,将![]() 绕点B逆时针旋转90°后得到△A′BC′.若反比例函数
绕点B逆时针旋转90°后得到△A′BC′.若反比例函数![]() 的图象恰好经过A’B的中点D,则k的值为( )
的图象恰好经过A’B的中点D,则k的值为( )
A.12B.15C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】伊利集团是中国规模最大、产品线最全的乳制品企业.综合实践小组的同学从网上搜集到如下一些伊利集团近几年的营业状况的资料,其中图1是2013-2018年伊利集团营业收入及净利润情况统计图,图2是2018年伊利集团各品类业务营业、收入比例情况统计图(数据来源:公司财报、中商产业研究院).
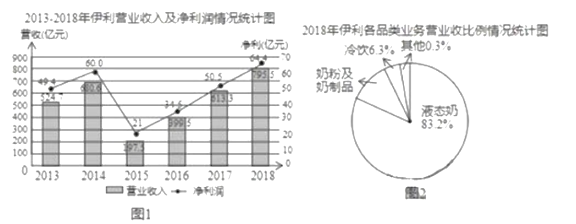
综合实践小组的同学结合统计图提出了如下问题,请你解答:
(1)2018年,伊利集团营收及净利再次刷新行业记录,稳居亚洲乳业第一,这一年,伊利集团实现营业收入 亿元,净利润 亿元.
(2)求2018年伊利集团“奶粉及奶制品”业务的营业收入(结果精确到![]() 亿元).
亿元).
(3)在2013-2018这![]() 年中,伊利集团的净利比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,并说明理由.
年中,伊利集团的净利比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com