
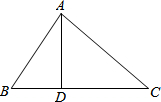
 如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=15,BD=5.
如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=15,BD=5. 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.
《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
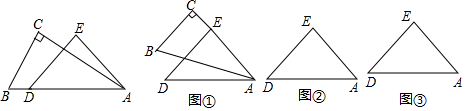
 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com