
ЁОЬтФПЁПвбжЊЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпLЃКy=x2-4x+3гыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌЖЅЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓЕуCКЭЕуAЕФзјБъЃЎ
ЃЈ2ЃЉЖЈвхЁАLЫЋХзЭМаЮЁБЃКжБЯпx=tНЋХзЮяЯпLЗжГЩСНВПЗжЃЌЪзЯШШЅЕєЦфВЛКЌЖЅЕуЕФВПЗжЃЌШЛКѓзїГіХзЮяЯпЪЃгрВПЗжЙигкжБЯпx=tЕФЖдГЦЭМаЮЃЌЕУЕНЕФећИіЭМаЮГЦЮЊХзЮяЯпLЙигкжБЯпx=tЕФЁАLЫЋХзЭМаЮЁБЃЈЬиБ№ЕиЃЌЕБжБЯпx=tЧЁКУЪЧХзЮяЯпЕФЖдГЦжсЪБЃЌЕУЕНЕФЁАLЫЋХзЭМаЮЁБВЛБфЃЉЃЌ
ЂйЕБt=0ЪБЃЌХзЮяЯпLЙигкжБевx=0ЕФЁАLЫЋХзЭМаЮЁБШчЭМЫљЪОЃЌжБЯпy=3гыЁАLЫЋХзЭМаЮЁБга______ИіНЛЕуЃЛ
ЂкШєХзЮяЯпLЙигкжБЯпx=tЕФЁАLЫЋХзЭМаЮЁБгыжБЯпy=3ЧЁКУгаСНИіНЛЕуЃЌНсКЯЭМЯѓЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃК______ЃЛ
ЂлЕБжБЯпx=tОЙ§ЕуAЪБЃЌЁАLЫЋХзЭМаЮЁБШчЭМЫљЪОЃЌЯжНЋЯпЖЮACЫљдкжБЯпбиЫЎЦНЃЈxжсЃЉЗНЯђзѓгвЦНвЦЃЌНЛЁАLЫЋХзЭМаЮЁБгкЕуPЃЌНЛxжсгкЕуQЃЌТњзуPQ=ACЪБЃЌЧѓЕуPЕФзјБъЃЎ

ЁОД№АИЁПЃЈ1ЃЉCЃЈ2ЃЌ-1ЃЉЃЌAЃЈ1ЃЌ0ЃЉЃЛЃЈ2ЃЉЂй3ЃЌЂк0ЃМtЃМ4ЃЌЂлЃЈ![]() +2ЃЌ1ЃЉЛђЃЈ-
+2ЃЌ1ЃЉЛђЃЈ-![]() +2ЃЌ1ЃЉЛђЃЈ-1ЃЌ0ЃЉ
+2ЃЌ1ЃЉЛђЃЈ-1ЃЌ0ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉСюy=0ЕУЃКx2-4x+3=0ЃЌШЛКѓЧѓЕУЗНГЬЕФНтЃЌДгЖјПЩЕУЕНAЁЂBЕФзјБъЃЌШЛКѓдйЧѓЕУХзЮяЯпЕФЖдГЦжсЮЊx=2ЃЌзюКѓНЋx=2ДњШыПЩЧѓЕУЕуCЕФзнзјБъЃЛ
ЃЈ2ЃЉЂйХзЮяЯпгыyжсНЛЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌШЛКѓзіГіжБЯпy=3ЃЌШЛКѓевГіНЛЕуИіЪ§МДПЩЃЛЂкНЋy=3ДњШыХзЮяЯпЕФНтЮіЪНЧѓЕУЖдгІЕФxЕФжЕЃЌДгЖјПЩЕУЕНжБЯпy=3гыЁАLЫЋХзЭМаЮЁБЧЁКУга3ИіНЛЕуЪБtЕФШЁжЕЃЌШЛКѓНсКЯКЏЪ§ЭМЯѓПЩЕУЕНЁАLЫЋХзЭМаЮЁБгыжБЯпy=3ЧЁКУгаСНИіНЛЕуЪБtЕФШЁжЕЗЖЮЇЃЛЂлЪзЯШжЄУїЫФБпаЮACQPЮЊЦНааЫФБпаЮЃЌгЩПЩЕУЕНЕуPЕФзнзјБъЮЊ1ЃЌШЛКѓгЩКЏЪ§НтЮіЪНПЩЧѓЕУЕуPЕФКсзјБъЃЎ
ЃЈ1ЃЉСюy=0ЕУЃКx2-4x+3=0ЃЌНтЕУЃКx=1Лђx=3ЃЌ
ЁрAЃЈ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЮЊx=2ЃЌ
НЋx=2ДњШыХзЮяЯпЕФНтЮіЪНЕУЃКy=-1ЃЌ
ЁрCЃЈ2ЃЌ-1ЃЉЃЛ
ЃЈ2ЃЉЂйНЋx=0ДњШыХзЮяЯпЕФНтЮіЪНЕУЃКy=3ЃЌ
ЁрХзЮяЯпгыyжсНЛЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
ШчЭМЫљЪОЃКзїжБЯпy=3ЃЌ
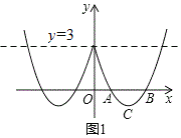
гЩЭМЯѓПЩжЊЃКжБЯпy=3гыЁАLЫЋХзЭМаЮЁБга3ИіНЛЕуЃЌ
ЙЪД№АИЮЊЃК3ЃЛ
ЂкНЋy=3ДњШыЕУЃКx2-4x+3=3ЃЌНтЕУЃКx=0Лђx=4ЃЌ
гЩКЏЪ§ЭМЯѓПЩжЊЃКЕБ0ЃМtЃМ4ЪБЃЌХзЮяЯпLЙигкжБЯпx=tЕФЁАLЫЋХзЭМаЮЁБгыжБЯпy=3ЧЁКУгаСНИіНЛЕуЃЌ
ЙЪД№АИЮЊЃК0ЃМtЃМ4ЃЎ
ЂлШчЭМ2ЫљЪОЃК
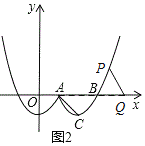
ЁпPQЁЮACЧвPQ=ACЃЌ
ЁрЫФБпаЮACQPЮЊЦНааЫФБпаЮЃЌ
гжЁпЕуCЕФзнзјБъЮЊ-1ЃЌ
ЁрЕуPЕФзнзјБъЮЊ1ЃЌ
НЋy=1ДњШыХзЮяЯпЕФНтЮіЪНЕУЃКx2-4x+3=1ЃЌНтЕУЃКx=![]() +2Лђx=-
+2Лђx=-![]() +2ЃЎ
+2ЃЎ
ЁрЕуPЕФзјБъЮЊЃЈ![]() +2ЃЌ1ЃЉЛђЃЈ-
+2ЃЌ1ЃЉЛђЃЈ-![]() +2ЃЌ1ЃЉЃЌ
+2ЃЌ1ЃЉЃЌ
ЕБЕуPЃЈ-1ЃЌ0ЃЉЪБЃЌвВТњзуЬѕМўЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуЃЈ![]() +2ЃЌ1ЃЉЛђЃЈ-
+2ЃЌ1ЃЉЛђЃЈ-![]() +2ЃЌ1ЃЉЛђЃЈ-1ЃЌ0ЃЉ
+2ЃЌ1ЃЉЛђЃЈ-1ЃЌ0ЃЉ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФвЛдЊЖўДЮЗНГЬx2+3x+m-1=0ЕФСНИіЪЕЪ§ИљЗжБ№ЮЊx1,x2ЃЎ
ЃЈ1ЃЉЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉШє2ЃЈx1+x2ЃЉ+ x1x2+10=0ЃЎЧѓmЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
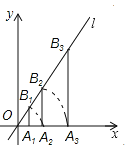
ЁОЬтФПЁПШчЭМЃЌЕуA1ЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЙ§ЕуA1зїxжсЕФДЙЯпНЛжБЯпlЃКy=![]() xгкЕуB1ЃЌвддЕуOЮЊдВаФЃЌOB1ЕФГЄЮЊАыОЖЛЛЁНЛxжсе§АыжсгкЕуA2ЃЛдйЙ§ЕуA2зїxжсЕФДЙЯпНЛжБЯпlгкЕуB2ЃЌвддЕуOЮЊдВаФЃЌвдOB2ЕФГЄЮЊАыОЖЛЛЁНЛxжсе§АыжсгкЕуA3ЃЛЁЃЎАДДЫзїЗЈНјааЯТШЅЃЌдђ
xгкЕуB1ЃЌвддЕуOЮЊдВаФЃЌOB1ЕФГЄЮЊАыОЖЛЛЁНЛxжсе§АыжсгкЕуA2ЃЛдйЙ§ЕуA2зїxжсЕФДЙЯпНЛжБЯпlгкЕуB2ЃЌвддЕуOЮЊдВаФЃЌвдOB2ЕФГЄЮЊАыОЖЛЛЁНЛxжсе§АыжсгкЕуA3ЃЛЁЃЎАДДЫзїЗЈНјааЯТШЅЃЌдђ![]() ЕФГЄЪЧ_____ЃЎ
ЕФГЄЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМдкжБНЧ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() жаЕуЃЌСЌНг
жаЕуЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЙ§Еу
ЕФжаЕуЃЌЙ§Еу![]() зї
зї![]() НЛЯпЖЮ
НЛЯпЖЮ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЃЈ2ЃЉдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГігы![]() УцЛ§ЯрЕШШ§НЧаЮЃЈВЛАќКЌ
УцЛ§ЯрЕШШ§НЧаЮЃЈВЛАќКЌ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
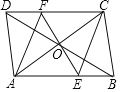
ЁОЬтФПЁПвбжЊЃКЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌЕуOЪЧЖдНЧЯпACЁЂBDЕФНЛЕуЃЌEFЙ§ЕуOЧвгыABЁЂCDЗжБ№ЯрНЛгкЕуEЁЂFЃЌСЌНгECЁЂAFЃЎ
ЃЈ1ЃЉЧѓжЄЃКDF=EBЃЛЃЈ2ЃЉAFгыЭМжаФФЬѕЯпЖЮЦНааЃПЧыжИГіЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГОАЧјдкЭЌвЛЯпТЗЩЯЫГДЮгаШ§ИіОАЕуAЃЌBЃЌCЃЌМзЁЂввСНУћгЮПЭДгОАЕуAГіЗЂЃЌМзВНааЕНОАЕуCЃЛввЛЈ20ЗжжгЪБМфХХЖгКѓГЫЙлЙтГЕЯШЕНОАЕуBЃЌдкBДІЭЃСєвЛЖЮЪБМфКѓЃЌдйВНааЕНОАЕуCЃЎМзЁЂввСНШЫРыОАЕуAЕФТЗГЬsЃЈУзЃЉЙигкЪБМфtЃЈЗжжгЃЉЕФКЏЪ§ЭМЯёШчЭМЫљЪОЃЎ
ЃЈ1ЃЉМзЕФЫйЖШЪЧ Уз/ЗжжгЃЛ
ЃЈ2ЃЉЕБ20Ёмt Ём30ЪБЃЌЧѓввРыОАЕуAЕФТЗГЬsгыtЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉввГіЗЂКѓЖрГЄЪБМфгыМздкЭОжаЯргіЃП
ЃЈ4ЃЉШєЕБМзЕНДяОАЕуCЪБЃЌввгыОАЕуCЕФТЗГЬЮЊ360УзЃЌдђввДгОАЕуBВНааЕНОАЕуCЕФЫйЖШЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
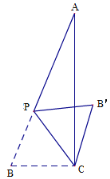
ЁОЬтФПЁПШчЭМЃЌдкЁїABC жаЃЌЁЯACBЃН90ЁуЃЌACЃН12ЃЌBCЃН5ЃЌP ЪЧБп AB ЩЯЕФЖЏЕуЃЈВЛгыЕу B жиКЯЃЉЃЌНЋЁїBCP би CP ЫљдкЕФжБЯпЗелЃЌЕУЕНЁїBЃЇCPЃЌСЌНг BЃЇAЃЌBЃЇA ГЄЖШЕФзюаЁжЕЪЧ mЃЌBЃЇA ГЄЖШЕФзюДѓжЕЪЧ nЃЌдђ m+n ЕФжЕЕШгк ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
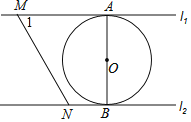
ЁОЬтФПЁПШчЭМЃЌжБЯп11ЁЮl2ЃЌЁбOгы11КЭl2ЗжБ№ЯрЧагкЕуAКЭЕуBЃЎЕуMКЭЕуNЗжБ№ЪЧl1КЭl2ЩЯЕФЖЏЕуЃЌMNбиl1КЭl2ЦНвЦЃЎЁбOЕФАыОЖЮЊ1ЃЌЁЯ1=60ЁуЃЎ
ЃЈ1ЃЉЕБMNгыЁбOЯрЧаЪБЃЌЧѓAMЕФГЄЃЛ
ЃЈ2ЃЉЕБЁЯMONЮЊЖрЩйЖШЪБЃЌMNгыЁбOЯрЧаЃЌВЂИјГіжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
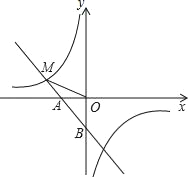
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y1ЃНЉxЉ1ЕФЭМЯѓгыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌгыЗДБШР§КЏЪ§![]() ЭМЯѓЕФвЛИіНЛЕуЮЊMЃЈЉ2ЃЌmЃЉЃЎ
ЭМЯѓЕФвЛИіНЛЕуЮЊMЃЈЉ2ЃЌmЃЉЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБy2ЃОy1ЪБЃЌЧѓxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЧѓЕуBЕНжБЯпOMЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com