
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象相交于A(-1,m),B(n,-1)两点,直线AB与y轴交于C点,连接OB.
的图象相交于A(-1,m),B(n,-1)两点,直线AB与y轴交于C点,连接OB.
(1)求一次函数的表达式;
(2)在x轴上找一点P,连接BP,使△BOP的面积等于△BOC的面积的2倍,求满足条件的点P的坐标.
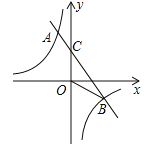
【答案】(1)y=-x+2;(2)P(12,0)或P(-12,0).
【解析】
(1)先利用反比例函数解析式确定A点和B点坐标,然后利用待定系数法求一次函数解析式;
(2)设P(t,0),先确定C(0,2),再计算出S△OBC=3,则利用题意得到![]() |t|1=6,然后解绝对值方程求出t,从而得到P点坐标.
|t|1=6,然后解绝对值方程求出t,从而得到P点坐标.
(1)把A(﹣1,m),B(n,﹣1)代入y![]() 得:m=3,n=3,∴A(﹣1,3),B(3,﹣1),把A(﹣1,3),B(3,﹣1)代入y=kx+b得:
得:m=3,n=3,∴A(﹣1,3),B(3,﹣1),把A(﹣1,3),B(3,﹣1)代入y=kx+b得:![]() ,解得:
,解得:![]() ,∴一次函数解析式为y=﹣x+2;
,∴一次函数解析式为y=﹣x+2;
(2)设P(t,0),当x=0时,y=﹣x+2=2,则C(0,2),∴S△OBC![]() 2×3=3.
2×3=3.
∵△BOP的面积等于△BOC面积的2倍,∴![]() |t|1=6,∴t=12或t=﹣12,∴P点坐标为(12,0)或(﹣12,0).
|t|1=6,∴t=12或t=﹣12,∴P点坐标为(12,0)或(﹣12,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了笔试与面试,甲、乙、丙三人的笔试成绩分别为95分、94分和94分.他们的面试成绩如表:
候选人 | 评委1 | 评委2 | 评委3 |
甲 | 94 | 89 | 90 |
乙 | 92 | 90 | 94 |
丙 | 91 | 88 | 94 |
(1)分别求出甲、乙、丙三人的面试成绩的平均分![]() 、
、![]() 、和
、和![]() ;
;
(2)若按笔试成绩的40%与面试成绩的60%的和作为综合成绩,综合成绩高者将被录用,请你通过计算判断谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.一个事件发生的机会是99.99%,所以我们说这个事件必然会发生
B.抛一枚硬币,出现正面朝上的机会是![]() ,所以连续抛2次,则必定有一次正面朝上
,所以连续抛2次,则必定有一次正面朝上
C.甲、乙两人掷一枚正六面体骰子做游戏,规则是:出现1点时甲赢,出现2点时乙赢,出现其它点数时大家不分输赢,这个游戏对两人来说是公平的
D.在牌面是1~9的九张牌中随机地抽出一张,抽到牌面是奇数和偶数的机会是一样的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一小长假的某一天,亮亮全家上午![]() 时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )

A.景点离亮亮的家![]() 千米
千米
B.亮亮到家的时间为![]() 时
时
C.小汽车返程的速度为![]() 千米/时
千米/时
D.![]() 时至
时至![]() 时,小汽车匀速行驶
时,小汽车匀速行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
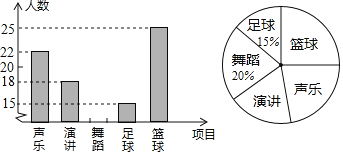
【题目】为丰富学生的文体生活,育红学校准备成立“声乐、演讲、舞蹈、足球、篮球”五个社团,要求每个学生都参加一个社团且每人只能参加一个社团.为了了解即将参加每个社团的大致人数,学校对部分学生进行了抽样调查在整理调查数据的过程中,绘制出如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生一共有多少人?
(2)将条形统计图补充完整.
(3)若全校有学生1500人,请你估计全校有意参加“声乐”社团的学生人数.
(4)从被抽查的学生中随意选出1人,该学生恰好选择参加“演讲”社团的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工地上有甲、乙二块铁板,铁板甲形状为等腰三角形,其顶角为![]() ,腰长为
,腰长为![]() ;铁板乙形状为直角梯形,两底边长分别为
;铁板乙形状为直角梯形,两底边长分别为![]() 、
、![]() ,且有一内角为
,且有一内角为![]() .现在我们把它们任意翻转,分别试图从一个直径为
.现在我们把它们任意翻转,分别试图从一个直径为![]() 的圆洞中穿过,结果是( )
的圆洞中穿过,结果是( )
A. 甲板能穿过,乙板不能穿过 B. 甲板不能穿过,乙板能穿过
C. 甲、乙两板都能穿过 D. 甲、乙两板都不能穿过
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边三角形
是等边三角形![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .以
.以![]() 为顶点,
为顶点,![]() 为一边,在
为一边,在![]() 外部作
外部作![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)根据推理可得![]() __________,
__________,![]() __________;(用含
__________;(用含![]() 的代数式表示)
的代数式表示)
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
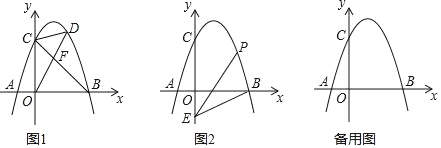
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com