
【题目】将正整数1至2018按一定的规律排成下图所示的10列,规定从上到下依次为1行、2行、3行…,从左到右依次为第1列至第10列.

(1)数2018在 行, 列;
(2)把图中带阴影的3个方相当作一个整体平移,设被框住的3个数中,最大的一个数为x.
①求被框住的三个数的和(用含x的式子表示);
②被框住的三个数的和能否于2017?若能,求出x的值;若不能,请说明理由.
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上任意一点,
边上任意一点,![]() 为
为![]() 边一动点,分别以
边一动点,分别以![]() 为边作等边三角形
为边作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() .
.

(1)试探索![]() 与
与![]() 的位置关系,并证明;
的位置关系,并证明;
(2)如图(2)当![]() 为
为![]() 延长线上任意一点时,(1)中的结论是否成立?请说明理由;
延长线上任意一点时,(1)中的结论是否成立?请说明理由;
(3)如图(3)在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 延长线上一点,
延长线上一点,![]() 为
为![]() 边一动点,分别以
边一动点,分别以![]() 为边作等腰三角形
为边作等腰三角形![]() 和等腰三角形
和等腰三角形![]() ,使得
,使得![]() ,连接
,连接![]() .要使(1)中的结论依然成立,还需要添加怎样的条件?为什么?
.要使(1)中的结论依然成立,还需要添加怎样的条件?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
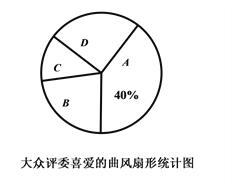
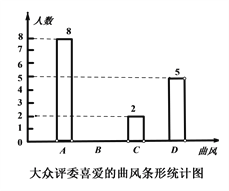
【题目】春雨初歇,绿意葱茏,重庆南开(融侨)中学初2020级举行了“春天的赞礼”为主题的合唱比赛,各班演唱歌曲的曲风有:青春舞曲、经典名曲、动漫神曲、励志金曲四种类型,为了了解同学们对各种曲风的喜爱程度。校学生处对大众评委喜爱的歌曲曲风进行了调查,(A—喜爱青春舞曲、B—喜爱经典名曲、C—喜爱动漫神曲、D—喜爱励志金曲),先根据调查得到如下图不完整的统计图,请结合图中信息完成下列问题:
![]() 扇形统计图中“C—喜爱动漫神曲”对应扇形圆心角为【1】度,并补全条形统计图.
扇形统计图中“C—喜爱动漫神曲”对应扇形圆心角为【1】度,并补全条形统计图.
![]() 在此次比赛中,甲班演唱的《四季问候》和乙班演唱的《东方之珠》获得一等奖,《司机问候》由2名男生和2名女生领唱,《东方之珠》由1名男生和2名女生领唱,校学生处打算分别从这两首歌曲的领唱中任意选取1名同学参加校合唱团,请用画树状图或列表的方法求出恰好选到1名男生和1名女生的概率.
在此次比赛中,甲班演唱的《四季问候》和乙班演唱的《东方之珠》获得一等奖,《司机问候》由2名男生和2名女生领唱,《东方之珠》由1名男生和2名女生领唱,校学生处打算分别从这两首歌曲的领唱中任意选取1名同学参加校合唱团,请用画树状图或列表的方法求出恰好选到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两实数a与b,M=![]() +
+![]() ,N=2ab
,N=2ab
(1)请判断M与N的大小,并说明理由。
(2)请根据(1)的结论,求![]() +
+![]() +3的最小值(其中x,y均为正数)
+3的最小值(其中x,y均为正数)
(3)请判断![]() +
+![]() +
+![]() abacbc的正负性(a,b,c为互不相等的实数)
abacbc的正负性(a,b,c为互不相等的实数)
(4)若n为正整数,则(n+1)(n+4)(n2+5n)+4的值为某一个整数的平方,试说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,①四边形ABCD是平行四边形,线段EF分别交AD、AC、BC于点E、O、F,②EF⊥AC,③AO=CO.
(1)求证:四边形AFCE是平行四边形;

(2)在本题①②③三个已知条件中,去掉一个条件,(1)的结论依然成立,这个条件是 (直接写出这个条件的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB=AC.延长BC到点D,使CD=CA,连接AD交⊙O于点E.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,BE=8,则EF的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com