
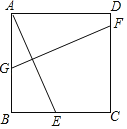
【题目】如图所示,正方形ABCD中,E为BC边上一点,连接AE,作AE的垂直平分线交AB于G,交CD于F,若BG=2BE,则DF:CF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
过点G作GH⊥CD于H,连接GE,可证△ABE≌△GHF,设BE=HF=x,通过BG=2BE,得到BG=2x,从而得到AG=GE=![]() ,然后再通过线段相等的关系得到DF和FC的长,即可得到答案.
,然后再通过线段相等的关系得到DF和FC的长,即可得到答案.
解:过点G作GH⊥CD于H,连接GE,则∠GHF=90°,即四边形AGHD为矩形,四边形BCHG为矩形,CH=BG,

∵GF垂直平分AE,四边形ABCD是正方形,
∴∠ABE=∠GHF=90°AB=AD=GH,AG=GE,
∵∠BAE+∠AGF=90°,∠AGF+∠FGH=90°,
∴∠BAE=∠FGH,
∴△ABE≌△GHF,
∴BE=HF,
设BE= HF =x,
∵BG=2BE,
∴BG=2x,即HC=2x,
∴FC=3x,
在直角三角形GBE中,![]() ,
,
∴AG=HD=![]() ,
,
DF=HD-HF=![]() ,
,
∴![]() ,
,
故选:A.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市体育中考现场考试内容有三项:50米跑为必测项目.另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.
(1)每位考生有_________种选择方案;
(2)求小明与小刚选择同种方案的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
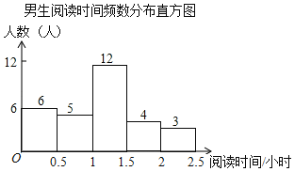
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
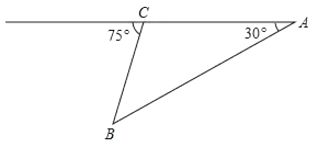
【题目】某国飞机失事坠入大海,该国立即派出一艘海上搜救船前往飞机失事海域进行打捞.在失事海域的![]() 点处仪器测得俯角为
点处仪器测得俯角为![]() 正前方的海底
正前方的海底![]() 点处有黑匣子,沿同一方向继续航行
点处有黑匣子,沿同一方向继续航行![]() 米到
米到![]() 点处,测得正前方
点处,测得正前方![]() 点处的俯角为
点处的俯角为![]() .求失事飞机的黑匣子离海面距离,(结果保留根号)(参考数据:
.求失事飞机的黑匣子离海面距离,(结果保留根号)(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=(ax-1)(x-a),其中a是常数,且a≠0.
(1)当a=2时,试判断点(-![]() ,-5)是否在该函数图象上.
,-5)是否在该函数图象上.
(2)若函数的图象经过点(1,-4),求该函数的表达式.
(3)当![]() -1≤x≤
-1≤x≤![]() +1时,y随x的增大而减小,求a的取值范围.
+1时,y随x的增大而减小,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O的两条弦AB,CD相交于点M,且AB=CD.
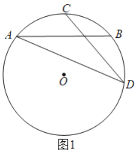
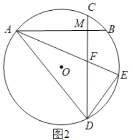
(1)如图1,连接AD.求证:AM=DM.
(2)如图2,若AB⊥CD,在弧BD上取一点E,使弧BE=弧BC,AE交CD于点F,连AD、DE.
①利断∠E与∠DFE是否相等,并说明理由.
②若DE=7,AM+MF=17,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如下不完整统计图.
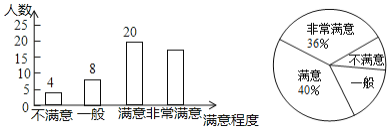
请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为多少人,其中“非常满意”的人数为多少人;
(2)兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访,已知这4位群众中有2位来自甲片区,另2位来自乙片区,请用画树状图或列表的方法求出选择的群众来自甲片区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,AD是角平分线,F为BA延长线上的一点,AE平分∠FAC,DE∥BA交AE于E.求证:四边形ADCE是矩形.
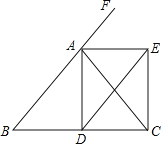
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com