
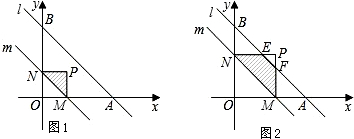
分析 (1)分别令直线l的解析式中x=0、y=0求出相对于的y、x的值,由此即可得出点A、B的坐标;
(2)假设能,根据平移的性质找出点P的坐标,利用三角形的面积公式求出S△MPN和S△OAB的值,根据两三角形面积间的关系找出关于t的一元二次方程,解方程求出点P的坐标,再验证点P是否在直线l的下方,由此即可得出结论;
(3)令点P在直线l上,求出此时t的值,根据重合部分的形状不同分两种情况讨论:①重合部分为△MPN,利用三角形的面积公式求出S△MPN;②重合部分为梯形MFEN,利用分割图形法结合三角形的面积公式求出S梯形MFEN.综合上面两种情况即可得出结论.
解答 解:(1)令y=-x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=-x+4中y=0,则-x+4=0,解得:x=4,
∴点A的坐标为(4,0).
(2)假设能,设直线m的解析式为y=-x+t,
则点M的坐标为(t,0)(t>0),点N的坐标为(0,t),
∴四边形OMPN为以MN为对角线的正方形形,
∴点M的坐标为(t,t),S△MPN=S△OMN=$\frac{1}{2}$OM•ON=$\frac{1}{2}{t}^{2}$.
∵S△OAB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×4×4=8,S△MPN=$\frac{3}{16}$S△OAB,即$\frac{1}{2}{t}^{2}$=$\frac{3}{16}$×8=$\frac{3}{2}$,
∴t=$\sqrt{3}$,或t=-$\sqrt{3}$(舍去),
∴此时点P的坐标为($\sqrt{3}$,$\sqrt{3}$).
将x=$\sqrt{3}$代入y=-x+4中得:y=4-$\sqrt{3}$,
∵4-$\sqrt{3}$>2>$\sqrt{3}$,
∴此时点P在直线l的下方.
故当△MPN完全夹在直线m和直线l之间时,△MPN的面积能达到△OAB面积的$\frac{3}{16}$,此时直线m的解析式为y=-x+$\sqrt{3}$.
(3)当点P(t,t)在直线l:y=-x+4上时,有t=-t+4,
解得:t=2.
△MPN和△OAB重合部分分两种情况:
①重合部分为△MPN,此时0<t≤2,如图1所示.
S△MPN=$\frac{1}{2}$t2;
②重合部分为梯形MFEN,此时2<t≤4,如图2所示.
S梯形MFEN=S△MPN-S△FPE=$\frac{1}{2}$t2-$\frac{1}{2}$(2t-4)2=-$\frac{3}{2}{t}^{2}$+8t-8.
综上可知:S与t的函数关系式为S=$\left\{\begin{array}{l}{\frac{1}{2}{t}^{2}(0<t≤2)}\\{-\frac{3}{2}{t}^{2}+8t-8(2<t≤4)}\end{array}\right.$.
点评 本题考查了一次函数与坐标轴的交点、正方形的性质、三角形的面积公式以及分割图形法求图形面积,解题的关键是:(1)分别代入x=0、y=0求值;(2)求出点P的坐标;(3)分情况讨论.本题属于中档题,难度不大,在该题中利用分割图形法求图形的面积是难点,在日常练习中应当加强练习.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
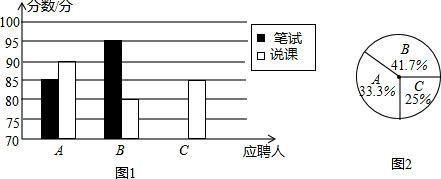
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 说课 | 80 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 学生 | A | B | C |
| 笔试成绩(单位:分) | 85 | 95 | 90 |
| 口试成绩(单位:分) | 90 | 80 | 85 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$
在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com