
【题目】如图,在平面直角坐标系中,矩形OABC的边OA与x轴重合,B的坐标为(﹣1,2),将矩形OABC绕平面内一点P顺时针旋转90°,使A、C两点恰好落在反比例函数![]() 的图象上,则旋转中心P点的坐标是( )
的图象上,则旋转中心P点的坐标是( )

A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
【答案】C
【解析】
设A'(a,![]() ),则C'(a+2,
),则C'(a+2,![]() -1),依据反比例函数图象上点的坐标特征,即可得到a=2,进而得出A'(2,2),C'(4,1),设P(x,y),再根据AP=A'P,CP=C'P,即可得到方程组
-1),依据反比例函数图象上点的坐标特征,即可得到a=2,进而得出A'(2,2),C'(4,1),设P(x,y),再根据AP=A'P,CP=C'P,即可得到方程组![]() ,进而得出旋转中心P点的坐标.
,进而得出旋转中心P点的坐标.
解:如图,
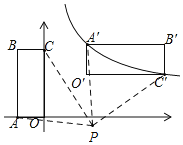
∵B的坐标为(-1,2),
∴矩形的长为2,宽为1,
由旋转可得,A'O'⊥x轴,O'C'⊥y轴,
设A'(a,![]() ),则C'(a+2,
),则C'(a+2,![]() -1),
-1),
∵点C'在反比例函数y=![]() 的图象上,
的图象上,
∴(a+2)(![]() -1)=4,
-1)=4,
解得a=2(负值已舍去),
∴A'(2,2),C'(4,1),
由旋转的性质可得,AP=A'P,CP=C'P,
设P(x,y),则
![]() ,
,
解得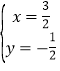 ,
,
∴旋转中心P点的坐标是(![]() ,-
,-![]() ),
),
故选:C.


科目:初中数学 来源: 题型:
【题目】如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据:![]() ,
,![]() ,
,![]() 结果精确到0.1小时)
结果精确到0.1小时)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的△ABC不是直角三角形的是()
A. BC=1,AC=2,AB=![]()
B. BC=1,AC=2,AB=![]()
C. BC:AC:AB=3:4:5
D. ∠A:∠B:∠C=3:4:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=60°,点D、E分别为边BC、AC上的点,连接DE,过点E作EF∥BC交AB于F,若BC=CE,CD=6,AE=8,∠EDB=2∠A,则BC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=![]() ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=![]() ,y=
,y=![]() .
.
启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD垂直BC于点D,且AD=BC,BC上方有一动点P满足![]() ,则点P到B、C两点距离之和最小时,∠PBC的度数为( )
,则点P到B、C两点距离之和最小时,∠PBC的度数为( )

A.30°B.45°C.60°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的较短对角线BD为4,∠ADB=60°,E、F分别在AD,CD上,且∠EBF=60°.
(1)求证:△ABE≌△DBF;
(2)判断△BEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销水杯,电热水壶两种商品,水杯每个进价15元,售价20元;电热水壶每个进价35元,售价45元.
(1)若该商场同时购进水杯、电热水壶共100件,恰好用去2700元,求能购进水杯、电热水壶各多少个?
(2)商场要求小明用1050元的钱(必须全部用完)采购水杯、电热水壶(或其中一种商品),且还要求总利润不少于340元(假设商品全部卖完),请你确定所有的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在直角坐标系中,四边形ABCO为正方形,A点的坐标为(a,0),D点的坐标为(0,b),且a,b满足(a﹣3)2+|b﹣![]() |=0.
|=0.
(1)求A点和D点的坐标;
(2)若∠DAE=![]() ∠OAB,请猜想DE,OD和EB的数量关系,说明理由.
∠OAB,请猜想DE,OD和EB的数量关系,说明理由.
(3)若∠OAD=30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com