
【题目】如图,在△ABC 中,D,E 分别是 AB,BC 上的点,且 DE∥AC,若 S△BDE:S△CDE=1:3,则S△DEB: S△ADC=( )

A. 1:5 B. 1:9 C. 1:10 D. 1:12
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )

A. 一直减小 B. 一直不变 C. 先减小后增大 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.(x2)3+(x3)2=2x6
B.(x2)3(x2)3=2x12
C.x4(2x)2=2x6
D.(2x)3(﹣x)2=﹣8x5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,不能应用平方差公式进行计算的是( )
A.(-x+2y)(2y+x)B.(x+y)(x-y)C.(a-b)(-a+b)D.(-2m+n)(-2m-n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读资料:小明是一个爱动脑筋的好学生,他在学习了有关圆的切线性质后,意犹未尽,又查阅到了与圆的切线相关的一个问题:
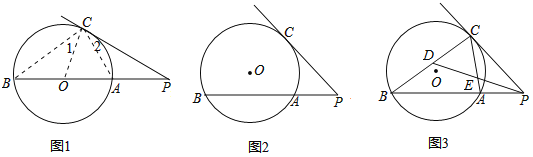
如图1,已知PC是⊙O的切线,AB是⊙O的直径,延长BA交切线PC与P,连接AC、BC、OC.
因为PC是⊙O的切线,AB是⊙O的直径,所以∠OCP=∠ACB=90°,所以∠1=∠2.
又因为∠B=∠1,所以∠B=∠2.
在△PAC与△PCB中,又因为:∠P=∠P,所以△PAC∽△PCB,所以![]() ,即PC2=PAPB.
,即PC2=PAPB.
问题拓展:
(Ⅰ)如果PB不经过⊙O的圆心O(如图2)等式PC2=PAPB,还成立吗?请证明你的结论;
综合应用:
(Ⅱ)如图3,⊙O是△ABC的外接圆,PC是⊙O的切线,C是切点,BA的延长线交PC于点P;
(1)当AB=PA,且PC=12时,求PA的值;
(2)D是BC的中点,PD交AC于点E.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com