
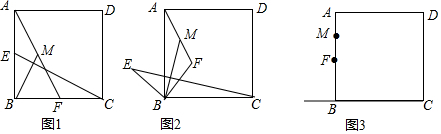
���� ��1������ȫ�������ε����ʵõ�CE=AF����BAF=��BCE������ֱ�������ε����ʵõ�BM=AM=$\frac{1}{2}$AF=$\frac{1}{2}$CE���õ���BAM=��ABM�����ݴ�ֱ�Ķ��弴�ɵ����ۣ�
��2����ͼ2���ӳ�AB��N��ʹNB=AB������FN���Ƴ�MBΪ��ANF����λ�ߣ�������������λ�ߵ����ʵõ�FN=2BM������ȫ�������ε����ʵõ�FN=CE���õ�CE=2BM������ƽ���ߵ����ʵõ���MBA=��N�����ɵ����ۣ�
��3���߶�CE��BM֮���������ϵû�з����仯�������߶μ��������ϵ�����������ɣ�
��� 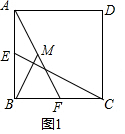 �⣺��1���߶�CE��BM֮���������ϵ��CE=2BM��λ�ù�ϵ��CE��BM��
�⣺��1���߶�CE��BM֮���������ϵ��CE=2BM��λ�ù�ϵ��CE��BM��
֤������ͼ1���ڡ�ABF���CBE�У�$\left\{\begin{array}{l}{AB=BC}\\{��ABC=��CBE}\\{BF=BE}\end{array}\right.$��
���ABF�ա�CBE��
��CE=AF����BAF=��BCE��
�ߵ�MΪAF�е㣬
��BM=AM=$\frac{1}{2}$AF=$\frac{1}{2}$CE��
���BAM=��ABM��
���BCE=��ABM��
�ߡ�BCE+��BEC=��BEC+��BCM=90�㣬
��BM��CE��
�ʴ�Ϊ��CE=2BM����ֱ��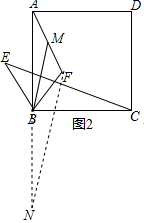
��2����1��������������Ȼ����������Ϊ��
֤������ͼ2���ӳ�AB��N��ʹNB=AB������FN��
��MΪAF�е㣬BΪAN�е㣬
��MBΪ��ANF����λ�ߣ�
��FN=2BM��
�ߡ�CBA=��CBN=��EBF=90�㣬
���ABC+��ABE=��CBN+��CBF������CBE=��NBF��
�ڡ�CBE�͡�FBN�У�$\left\{\begin{array}{l}{BC=BN}\\{��CBF=��NBF}\\{BE=BF}\end{array}\right.$��
���CBE�ա�FBN��SAS����
��FN=CE��
��CE=2BM��
��MBΪ��ANF����λ�ߣ�
��BM��FN��
���MBA=��N��
�֡ߡ�CBE�ա�NBF��
���BCE=��N��
�ߡ�MBA+��CBM=90�㣬
���ECB+��ABM=90�㣬��CE��BM��
��3���߶�CE��BM֮���������ϵû�з����仯���������£�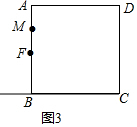
��ͼ3����AB=BC=a��BE=BF=b����CE=a+b��
�ߵ�MΪAF���е㣬
��MF=$\frac{1}{2}$��a-b����
��BC=b+$\frac{1}{2}$��a-b��=$\frac{1}{2}$��a+b����
��CE=2BM��
���� ���⿼���˼��α任�ۺ��⣬�漰��֪ʶ�У�ȫ�������ε��ж������ʣ�����ֱ�������ε��ж������ʣ������ε���λ�߶�������һ����֪ʶ��̽�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
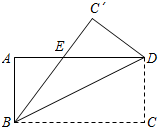 �Ѿ���ABCD���ŶԽ���BD�۵���ʹ��C����C�䴦����AD��E����AD=8��AB=4����AE�ij�Ϊ��������
�Ѿ���ABCD���ŶԽ���BD�۵���ʹ��C����C�䴦����AD��E����AD=8��AB=4����AE�ij�Ϊ��������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�٣�AE�ǡ�O��ֱ������C�ǡ�O�ϵĵ㣬����AC���ӳ�AC����D��ʹCD=CA������ED����O�ڵ�B��
��ͼ�٣�AE�ǡ�O��ֱ������C�ǡ�O�ϵĵ㣬����AC���ӳ�AC����D��ʹCD=CA������ED����O�ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
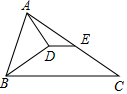 ��ͼ����ABC�У�BDƽ�֡�ABC����AD��BD��EΪAC���е㣬AD=6cm��BD=8cm��BC=16cm����DE�ij�Ϊ3cm��
��ͼ����ABC�У�BDƽ�֡�ABC����AD��BD��EΪAC���е㣬AD=6cm��BD=8cm��BC=16cm����DE�ij�Ϊ3cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
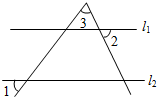 ��ͼ��ֱ��l1��l2����1=55�㣬��3=65�㣬���2��СΪ��������
��ͼ��ֱ��l1��l2����1=55�㣬��3=65�㣬���2��СΪ��������| A�� | 50�� | B�� | 55�� | C�� | 60�� | D�� | 65�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com