
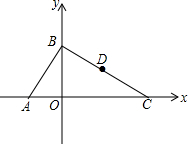
 Èçͼ£¬ÔÚƽĂæÖ±½Ç×ø±êϵÖĐ£¬µăOΪ×ø±êÔµă£¬Ö±Ïßy=$\sqrt{3}$x+2$\sqrt{3}$ÓëxÖá¡¢yÖá·Ö²¼½»ÓÚA¡¢BÁ½µă£¬¹ưµăB×÷ABµÄ´¹Ïߣ¬½»xÖáÓÚµăC£¬µăDΪBCÖĐµă£®
Èçͼ£¬ÔÚƽĂæÖ±½Ç×ø±êϵÖĐ£¬µăOΪ×ø±êÔµă£¬Ö±Ïßy=$\sqrt{3}$x+2$\sqrt{3}$ÓëxÖá¡¢yÖá·Ö²¼½»ÓÚA¡¢BÁ½µă£¬¹ưµăB×÷ABµÄ´¹Ïߣ¬½»xÖáÓÚµăC£¬µăDΪBCÖĐµă£®·ÖÎö £¨1£©ÏÈÇóµĂµăA¡¢BµÄ×ø±ê£¬È»ºóÓÉÉäÓ°¶¨ÀíÇóµĂOCµÄ³¤£¬´Ó¶ø¿ÉÇóµĂµăDµÄ×ø±ê£»
£¨2£©Èçͼ1Ëùʾ£¬¹ưµăE×÷BEµÄ´¹Ïß½»Ö±ÏßBCÓëµăG£¬Ê×ÏÈÖ¤Ă÷¡÷BPE¡×¡÷GQE£¬È»ºóÓÉÏàËÆÈư½ÇĐεÄĐÔÖÊ¿ÉÇóµĂtan¡ÏEBG=$\sqrt{3}$£¬´Ó¶ø¿ÉÇóµĂBE=$\frac{\sqrt{3}}{2}$BG£»Èçͼ2£¬µ±µăEÔÚµăB×ó±ßʱ£¬BG=DQ+GQ-BD=2t-2$\sqrt{3}$£¬ÓÉBE=$\frac{\sqrt{3}}{2}BG$´Ó¶ø¿ÉÇóµĂº¯Êư¹Øϵʽ£»
£¨3£©Èçͼ3Ëùʾ£ºµ±¡ÏAED=90¡ăʱ£¬Ö¤Ă÷¡÷PAE¡×¡÷QDE£¬ÓÉÏàËÆÈư½ÇĐεÄĐÔÖÊ¿ÉÇóµĂt=$\frac{2\sqrt{3}}{3}$£»Èçͼ4£¬µ±¡ÏADE=90¡ăʱ£¬ÑÓ³¤FD½»Ö±ÏßBEÓëN£¬Ê×ÏÈÖ¤Ă÷¡÷ADF¡×¡÷DEN£¬´Ó¶ø¿ÉÇóµĂEN=$\frac{3}{5}$£¬ÓÉBN=$\frac{\sqrt{3}}{2}DB$¿ÉÇóµĂBN=3£¬ÓÉBE=BN-EN¿ÉÖª3-$\sqrt{3}t$=$\frac{12}{5}$£®
½â´đ ½â£º£¨1£©Áîx=0µĂy=2$\sqrt{3}$£¬
¡àµăBµÄ×ø±êΪ£¨0£¬2$\sqrt{3}$£©£®
Áîy=0µĂ£»$\sqrt{3}$x+2$\sqrt{3}$=0£¬½âµĂ£ºx=-2£®
¡àµăAµÄ×ø±êΪ£¨-2£¬0£©£®
¡ßAB¡ÍBC£¬
ÓÉÉäÓ°¶¨ÀíµĂ£ºOB2=OA•OC£®
¡à$£¨2\sqrt{3}£©^{2}=2¡ÁOC$£®
½âµĂ£ºOC=6£®
¡ßµăDÊÇBCµÄÖĐµă£¬
¡àµăDµÄ×ø±êÊÇ£¨3£¬$\sqrt{3}$£©£®
£¨2£©Èçͼ1Ëùʾ£¬¹ưµăE×÷BEµÄ´¹Ïß½»Ö±ÏßBCÓëµăG£®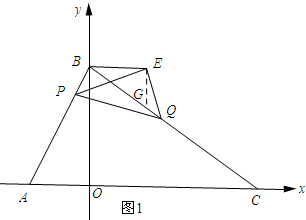
¡ß¡ÏBEG=¡ÏPEQ£¬
¡à¡ÏBEP=¡ÏGEQ£®
¡ß¡ÏPBC=¡ÏPEQ£¬
¡à¡ÏBPE=¡ÏGQE£®
¡à¡÷BPE¡×¡÷GQE£®
¡àGQ=$\frac{\sqrt{3}}{3}BP=\frac{\sqrt{3}}{3}¡Á\sqrt{3}t$=t£®
¡ßDQ=t£¬BG=BD-DQ-GQ=2$\sqrt{3}$-t-t=2$\sqrt{3}$-2t£®
¡ß¡÷BPE¡×¡÷GQE£¬
¡à$\frac{BE}{GE}=\frac{PE}{QE}$=$\sqrt{3}$£®
¡à¡ÏEBG=30¡ă£®
¡àBE=$\frac{\sqrt{3}}{2}$BG=3$-\sqrt{3}$t£¨0¡Üt$£¼\sqrt{3}$£©£®
Èçͼ2£¬µ±µăEÔÚµăB×ó±ßʱ£®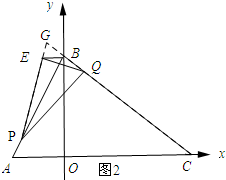
¡ßBG=DQ+GQ-BD=t+t-2$\sqrt{3}$=2t-2$\sqrt{3}$£®
¡àBE=$\frac{\sqrt{3}}{2}BG$=$\sqrt{3}t-3$£¨$\sqrt{3}£¼t¡Ü\frac{4\sqrt{3}}{3}$£©£®
¡àdÓëtµÄº¯Êư¹ØϵʽΪd=$\left\{\begin{array}{l}{3-\sqrt{3}t£¨0¡Üt£¼\sqrt{3}£©}\\{\sqrt{3}t-3£¨\sqrt{3}£¼t¡Ü\frac{4\sqrt{3}}{3}£©}\end{array}\right.$
£¨3£©½â£ºÈçͼ3Ëùʾ£ºµ±¡ÏAED=90¡ăʱ£¬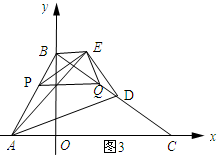
¡ß¡ÏPEQ=90¡ă£¬
¡à¡ÏPEA=¡ÏQED£®
ÓÖ¡ß¡ÏPAE=¡ÏQDE£¬
¡à¡÷PAE¡×¡÷QDE£®
¡à$\frac{PA}{QD}=\frac{PE}{QE}$£®
¡à$\frac{4-\sqrt{3}t}{t}=\sqrt{3}$£®
¡àt=$\frac{2\sqrt{3}}{3}$£®
Èçͼ4£¬µ±¡ÏADE=90¡ăʱ£¬ÑÓ³¤FD½»Ö±ÏßBEÓëN£®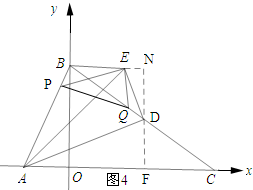
¡ß¡ÏPAE=¡ÏQED£¬
¡àBE¡ÎOC£®
¡à¡ÏEN=¡ÏAFD=90¡ă£®
¡ß¡ÏADF+¡ÏEDN=90¡ă£¬¡ÏNED+¡ÏEDN=90¡ă£¬
¡à¡ÏADF=¡ÏNED£®
¡à¡÷ADF¡×¡÷DEN£®
¡à$\frac{EN}{DF}=\frac{DN}{AF}$£®
¡ßDN=$\frac{1}{2}BD$=$\sqrt{3}$£¬
¡à$\frac{EN}{\sqrt{3}}=\frac{\sqrt{3}}{5}$£®
¡àEN=$\frac{3}{5}$£®
¡ßBN=$\frac{\sqrt{3}}{2}DB=\frac{\sqrt{3}}{2}¡Á2\sqrt{3}=3$
¡àBE=BN-EN=3-$\frac{3}{5}$=$\frac{12}{5}$£®
¡à3-$\sqrt{3}t$=$\frac{12}{5}$£®
½âµĂ£ºt=$\frac{\sqrt{3}}{5}$£®
µăP¡¢QÔÚÔ˶¯¹ư³̀ÖĐ²»´æÔÚ̉Ô¡ÏDAEΪֱ½ÇµÄÇé¿ö£®
×ÛÉÏËùÊö£¬t=$\frac{2\sqrt{3}}{3}$Ă룬»̣t=$\frac{\sqrt{3}}{5}$Ăëʱ£¬¡÷ADEΪֱ½ÇÈư½ÇĐΣ®
µăÆÀ ±¾̀âÖ÷̉ª¿¼²éµÄÊÇ̉»´Îº¯ÊưµÄ×ÛºÏÓ¦ÓĂ¡¢½â´đ±¾̀âÖ÷̉ªÓ¦ÓĂÁËÉäÓ°¶¨Àí¡¢̀ØÊâÈñ½ÇÈư½Çº¯ÊưÖµ¡¢ÏàËÆÈư½ÇĐεÄĐÔÖʺÍÅж¨£¬¸ù¾Ừẩ⻳ö·ûºÏ̀ẩâµÄͼĐÎÊǽâ´đ±¾̀âµÄ¹Ø¼ü£®


 ÔĶÁ¿́³µÏµÁĐ´đ°¸
ÔĶÁ¿́³µÏµÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 4-2a | B£® | 0 | C£® | 2a-4 | D£® | 4 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
°Ù¶ÈÖÂĐÅ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com