
【题目】在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=22.5°,E在AB上,且∠DCE=67.5°,DE⊥AB于E,若AE=1,线段BE的长为____________.

【答案】![]() .
.
【解析】由∠CAB=∠CAD=22.5°可得∠DAE=45°,DE⊥AB,所以DE=AE=1.根据勾股定理可求得AD=6,由∠CAB=∠CAD=22.5°,再根据角的平分线上的点到角的两边的距离相等,可证得BC=CF,然后证得△CBG≌△CFD,再证得△CGE≌△CED,求得∠3=∠4=45°,从而求得CE=AE=1,在△CBE中根据勾股定理求得BE的长.
∵∠CAB=∠CAD=22.5°,
∴∠DAE=45°,
又∵∠AED=90°,
∴DE=AE=1,
∴AD=![]() .
.
延长AD,过点C作CF垂直AD于F,
由∠CAB=∠CAD可知AC为∠BAD的角平分线,
∴CB=CF,
把三角形CDF绕点C旋转到CF与CB重合,则DF与GB重合,如图:
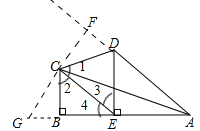 .
.
∴CG=CD,∠GCB=∠DCF;
∵CB⊥AB,CF⊥AD,∠CAB=∠CAD=22.5°;
∴∠ACB=∠ACF=67.5°=∠DCE
∴∠DCA=∠2=∠3,∠DCA+∠DCF=∠2+∠GCB=∠DCE=67.5°,
在△DCE与△GCE中
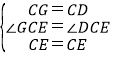 ,
,
∴△DCE≌△GCE(SAS),
∴∠3=∠4=45°,
∵∠CAB=∠CAD=22.5°,∠4=∠CAB+∠ACE,
∴∠ACE=∠CAB=22.5°,
∴CE=AE=1,
在Rt△CBE中,BE2+BC2=CE2,
即BE=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,8)、B(8,0)、E(-2,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒2个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒。
(1)填空:直线AB的解析式是_____________________;
(2)求t的值,使得直线CD∥AB;
(3)是否存在时刻t,使得△ECD是等腰三角形?若存在,请求出一个这样的t值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
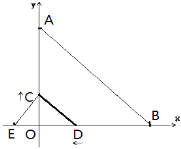
【题目】已知:如图,在ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.
求证:四边形AGCH是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP= ![]() ;④S四边形ECFG=2S△BGE .
;④S四边形ECFG=2S△BGE . 
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,绵阳市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: 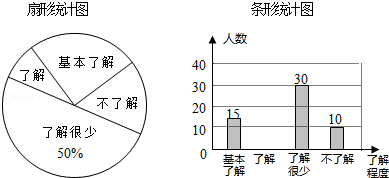
(1)接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;
(2)请补全条形统计图;
(3)若该中学共有学生3000人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() ,
, ![]() ,试说明:BE∥CF.
,试说明:BE∥CF.
完善下面的解答过程,并填写理由或数学式:
解:∵ ![]() (已知)
(已知)
∴AE∥ ( )
∴![]() ( )
( )
∵![]() (已知)
(已知)
∴![]() ( )
( )
∴DC∥AB( )
∴![]() ( )
( )
即![]()
∵![]() (已知)
(已知)
∴![]() ( )
( )
即![]()
∴BE∥CF( ) .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( ) 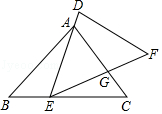
A.![]() =
= ![]()
B.![]() =
= ![]()
C.![]() =
= ![]()
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
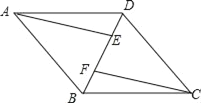
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com