
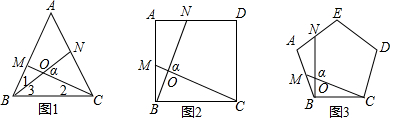
分析 (1)根据正方形的性质得到AB=BC,∠A=∠CBM=90°,根据全等三角形的性质得到∠1=∠2,根据三角形的外角的性质即可得到结论;
(2))由于四边形ABCD是正五边形,得到AB=BC,∠A=∠CBM=108°,根据全等三角形的性质得到∠1=∠2,根据三角形的外角的性质即可得到结论;
(3)根据(1)、(2)的结论即可得到结果.
解答 解: (1)∵四边形ABCD是正方形,
(1)∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBM=90°,
在△ABN与△BCM中,$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠CBM}\\{AN=BM}\end{array}\right.$,
∴△ABN≌△BCM,
∴∠1=∠2,
∵∠α是△BOC的外角,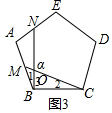
∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=90°;
故答案为:90;
(2))∵四边形ABCD是正五边形,
∴AB=BC,∠A=∠CBM=108°,
在△ABN与△BCM中,$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠CBM}\\{AN=BM}\end{array}\right.$,
∴△ABN≌△BCM,
∴∠1=∠2,
∵∠α是△BOC的外角,
∴∠α=∠2+∠3,
∴∠α=∠1+∠3=∠ABC=108°;
故答案为:108;
(3)∠α可以等于160°,
理由:由于上述操作发现的结论可知,正n边形中的∠α=正n边形的内角的度数,
假设存在正n边形使得∠α=160°,则(n-2)•180°=160°n,
解得:n=18,
∴存在正n边形使得∠α=160°,
此时,该正n边形为正十八边形.
点评 本题考查了正多边形的性质,全等三角形的判定和性质,三角形的外角的性质,熟练掌握全等三角形的判定和性质是解题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
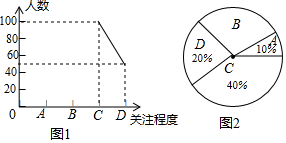
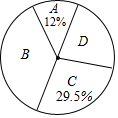 某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.
某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.| 分组 | 次数x(个) | 人数 |
| A | 0≤x<120 | 24 |
| B | 120≤x<130 | 72 |
| C | 130≤x<140 | |
| D | x≥140 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com