
 一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为$\frac{40+40\sqrt{3}}{3}$海里/小时.
一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为$\frac{40+40\sqrt{3}}{3}$海里/小时. 分析 设该船行驶的速度为x海里/时,由已知可得BC=3x,AQ⊥BC,∠BAQ=60°,∠CAQ=45°,AB=80海里,在直角三角形ABQ中求出AQ、BQ,再在直角三角形AQC中求出CQ,得出BC=40+40$\sqrt{3}$=3x,解方程即可.
解答 解:如图所示:
设该船行驶的速度为x海里/时,
3小时后到达小岛的北偏西45°的C处,
由题意得:AB=80海里,BC=3x海里,
在直角三角形ABQ中,∠BAQ=60°,
∴∠B=90°-60°=30°,
∴AQ=$\frac{1}{2}$AB=40,BQ=$\sqrt{3}$AQ=40$\sqrt{3}$,
在直角三角形AQC中,∠CAQ=45°,
∴CQ=AQ=40,
∴BC=40+40$\sqrt{3}$=3x,
解得:x=$\frac{40+40\sqrt{3}}{3}$.
即该船行驶的速度为$\frac{40+40\sqrt{3}}{3}$海里/时;
故答案为:$\frac{40+40\sqrt{3}}{3}$.
点评 本题考查了解直角三角形的应用中的方向角问题、等腰直角三角形的性质、含30°角的直角三角形的性质等知识;通过解直角三角形得出方程是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )| A. | 该村人均耕地面积随总人口的增多而增多 | |
| B. | 该村人均耕地面积y与总人口x成正比例 | |
| C. | 若该村人均耕地面积为2公顷,则总人口有100人 | |
| D. | 当该村总人口为50人时,人均耕地面积为1公顷 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠α、∠β.
如图,已知∠α、∠β.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b=2,c=3 | B. | b=-4,c=3 | C. | b=-2,c=-3 | D. | b=-4,c=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 大瓶 | 小瓶 | |
| 进价(元/瓶) | 5 | 2 |
| 售价(元/瓶) | 7 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
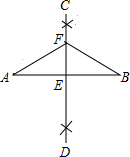 如图,已知线段AB,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB=5.
如图,已知线段AB,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com