
 ,求△CAF的面积.
,求△CAF的面积.
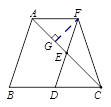
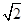 ,在Rt△FGC中应用勾股定理求得GC的长,即可得AC=AG+GC=
,在Rt△FGC中应用勾股定理求得GC的长,即可得AC=AG+GC=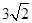 ,从而求得△CAF的面积.
,从而求得△CAF的面积.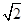 .
.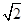 ,CF=
,CF= ,
, .
.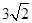 .
.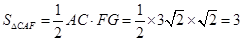 .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
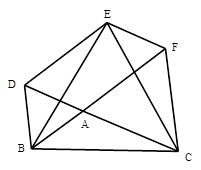
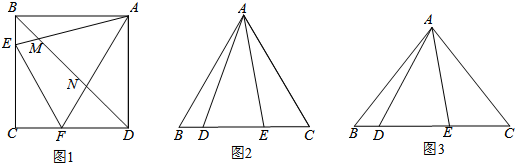
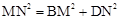 ,请证明这个等量关系;
,请证明这个等量关系;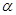 ,(0°<
,(0°<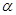 <90°),∠DAE=
<90°),∠DAE=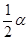 时,BD、DE、EC应满足的等量关系是____________________.【参考:
时,BD、DE、EC应满足的等量关系是____________________.【参考: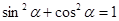 】
】
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
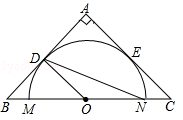
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
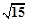 (B)8 (C)2
(B)8 (C)2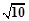 (D)2
(D)2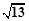
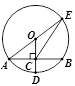
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.10cm. | B.24cm | C.26cm. | D.52cm. |
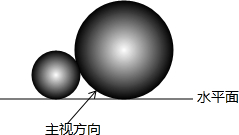
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com