
 如图,直线l:y=-x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
如图,直线l:y=-x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.分析 (1)先求出A、B坐标,再求出OB、OA、AB即可解决问题.
(2)由△PBO∽△OAQ,得$\frac{PB}{OA}$=$\frac{OB}{AQ}$,求出PB,再根据等腰直角三角形性质可以求得点P坐标.
(3)先求出m的值,分①a>0,②a<0,两种情形,利用二次函数性质分别求解即可.
解答 解:(1)在函数y=-x+1中,令x=0,得y=1,
∴B(0,1),
令y=0,得x=1,
∴A(1,0),
则OA=OB=1,AB=$\sqrt{2}$,
∴△AOB周长为1+1+$\sqrt{2}$=2+$\sqrt{2}$.
(2)∵OA=OB,
∴∠ABO=∠BAO=45°,
∴∠PBO=∠QAO=135°,
设∠POB=x,则∠OPB=∠AOQ=135°-x-90°=45°-x,
∴△PBO∽△OAQ,
∴$\frac{PB}{OA}$=$\frac{OB}{AQ}$,
∴PB=$\frac{OA•OB}{AQ}$=$\frac{1}{t}$,
过点P作PH⊥OB于H点,
则△PHB为等腰直角三角形,
∵PB=$\frac{1}{t}$,
∴PH=HB=$\frac{\sqrt{2}}{2t}$,
∴P(-$\frac{\sqrt{2}}{2t}$,1+$\frac{\sqrt{2}}{2t}$).
(3)由(2)可知△PBO∽△OAQ,若它们的周长相等,则相似比为1,即全等,
∴PB=OA,
∴$\frac{1}{t}$=1,
∴t=1,
同理可得Q(1+$\frac{\sqrt{2}}{2t}$,-$\frac{\sqrt{2}}{2t}$),
∴m=$\frac{\frac{\sqrt{2}}{2t}}{1+\frac{\sqrt{2}}{2t}}$=$\sqrt{2}$-1,
∵抛物线经过点A,
∴a+b+c=0,
又∵6a+3b+2c=0,
∴b=-4a,c=3a,
对称轴x=2,取值范围$\sqrt{2}$-1≤x$≤\sqrt{2}$+1,
①若a>0,则开口向上,
由题意x=$\sqrt{2}$-1时取得最大值$\frac{2}{m}$=2$\sqrt{2}$+2,
即($\sqrt{2}$-1)2a+($\sqrt{2}$-1)b+c=2$\sqrt{2}$+2,
解得a=$\frac{11+8\sqrt{2}}{7}$.
②若a<0,则开口向下,
由题意x=2时取得最大值2$\sqrt{2}$+2,
即4a+2b+c=2$\sqrt{2}$+2,
解得a=-2$\sqrt{2}$-2.
综上所述所求a的值为$\frac{11+8\sqrt{2}}{7}$或-2$\sqrt{2}$-2.
点评 本题考查二次函数综合题、相似三角形的判定和性质、等腰直角三角形的性质、函数最值问题等知识,解题的关键是灵活应用这些知识解决问题,学会分类讨论,考虑问题要全面,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| 甲方案 | 乙方案 | |
| 门号的月租费(元) | 400 | 600 |
| MAT手机价格(元) | 15000 | 13000 |
| 注意事项:以上方案两年内不可变更月租费 | ||
| A. | 500 | B. | 516 | C. | 517 | D. | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
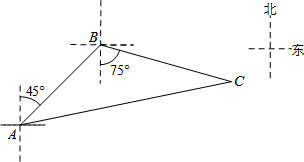 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
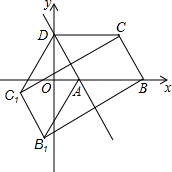 如图,已知?ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D
如图,已知?ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
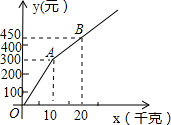 甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向上,顶点坐标为(-1,-4) | B. | 开口向下,顶点坐标为(1,4) | ||
| C. | 开口向上,顶点坐标为(1,4) | D. | 开口向下,顶点坐标为(-1,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com