
【题目】猜想与证明:小强想证明下面的问题:“有两个角(图中的![]() 和
和![]() )相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的
)相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的![]() 和边
和边![]() .
.
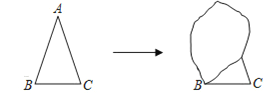
(1)请问:他能够把图恢复成原来的样子吗?若能,请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子.

(2)你能够证明这样的三角形是等腰三角形吗?(至少用两种方法证明)

【答案】(1)能,具体见解析;(2)证明见解析.
【解析】
(1)方法1:量出 ∠C的大小;作∠B =∠C;则∠B的一条边和∠C的一条边的延长线交于点A;方法2:作边BC的垂直平分线与∠C的另一边的延长线交于点A,连接AB即可;方法3:将长方形纸片对折使点B和点C重合,找到∠ C的另一边的延长线与折痕的交点A,连接AB即可;
(2)证法1:作∠A的平分线AD,交BC与点D,利用AAS即可证出△ABD≌△ACD,从而得出AB=AC,根据等腰三角形的定义即可得出结论;证法2:过A作AD⊥BC于D,利用AAS即可证出△ABD≌△ACD,从而得出AB=AC,根据等腰三角形的定义即可得出结论.
解:(1)方法1:量出 ∠C的大小;作∠B =∠C;则∠B的一条边和∠C的一条边的延长线交于点A.如下图所示:△ABC即为所求
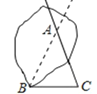
方法2:作边BC的垂直平分线与∠C的另一边的延长线交于点A,连接AB,如下图所示:△ABC即为所求.
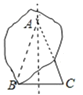
方法3:如图,将长方形纸片对折使点B和点C重合,找到∠ C的另一边的延长线与折痕的交点A,连接AB,如下图所示:△ABC即为所求

(2)证法1:作∠A的平分线AD,交BC与点D
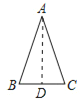
∴∠BAD=∠CAD
在△ABD和△ACD中

∴△ABD≌△ACD
∴AB=AC,
即△ABC为等腰三角形;
证法2:过A作AD⊥BC于D,

∴∠ADB=∠ADC=90°
在△ABD和△ACD中
∴△ABD≌△ACD
∴AB=AC,
即△ABC为等腰三角形.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
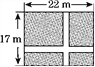
【题目】如图,在一块长为22 m,宽为17 m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300 m2.若设道路宽为x m,根据题意可列出方程为______________________________.
【答案】(22-x)(17-x)=300(或x2-39x+74=0)
【解析】试题分析:把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程.设道路的宽应为x米,由题意有(22﹣x)(17﹣x)=300,故答案为:(22﹣x)(17﹣x)=300.
考点:由实际问题抽象出一元二次方程.
【题型】填空题
【结束】
17
【题目】x=1是关于x的一元二次方程x2+mx﹣5=0的一个根,则此方程的另一个根是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D,旋转角为![]() .
.
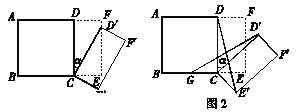
(1)当点D′恰好落在EF边上时,则旋转角α的值为________度;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,是否存在旋转角α,使△DCD′与△CBD′全等?若能,直接写出旋转角α的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 的坐标为
的坐标为![]() ,将点
,将点![]() 向右平移
向右平移![]() 个单位得到点
个单位得到点![]() ,其中关于
,其中关于![]() 的一元一次不等式
的一元一次不等式![]() 的解集为
的解集为![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() .
.
(1)求![]() 两点坐标及四边形
两点坐标及四边形![]() 的面积;
的面积;
(2)如图2,点![]() 自
自![]() 点以1个单位/秒的速度在
点以1个单位/秒的速度在![]() 轴上向上运动,点
轴上向上运动,点![]() 自
自![]() 点以2个单位/秒的速度在
点以2个单位/秒的速度在![]() 轴上向左运动,设运动时间为
轴上向左运动,设运动时间为![]() 秒(
秒(![]() ),是否存在一段时间使得
),是否存在一段时间使得![]() ,若存在,求出
,若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)在(2)的条件下,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示8×7的正方形网格中,A(2,0),B(3,2),C(4,2),请按要求解答下列问题:

(1)将△ABO向右平移4个单位长度得到△A1B1O1,请画出△A1B1O1并写出点A1的坐标;
(2)将△ABO绕点C(4,2)顺时针旋转90°得到△A2B2O2,请画出△A2B2O2并写出点A2的坐标;
(3)将△A1B1O1绕点Q旋转90°可以和△A2B2O2完全重合,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人寿保险公司的一张关于某地区的生命表的部分摘录如下:
年龄 | 活到该年龄的人数 | 在该年龄的死亡人数 |
40 | 80500 | 892 |
50 | 78009 | 951 |
60 | 69891 | 1200 |
70 | 45502 | 2119 |
80 | 16078 | 2001 |
… | … | … |
根据上表解下列各题:
(1)某人今年50岁,他当年去世的概率是多少?他活到80岁的概率是多少?
(保留三个有效数字)
(2)如果有20000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,预计保险公司需付赔偿的总额为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com