
分析 (1)利用因式分解法求出方程的两根,再根据倍根方程的定义判断即可;
(2)根据倍根方程的定义得到x1,x2,得到$\frac{n}{m}$=-1,或$\frac{n}{m}$=-4,即可得到4m2+5mn+n2=0;
(3)由方程ax2+bx+c=0是倍根方程,得到x1=2x2,有已知条件得到得到抛物线的对称轴x=$\frac{5}{2}$,于是求出x1=$\frac{5}{3}$.
解答 解:(1)是倍根方程,理由如下:
解方程x2-3x+2=0,得x1=1,x2=2,
∵2是1的2倍,
∴一元二次方程x2-3x+2=0是倍根方程;
(2)∵(x-2)(mx+n)=0是倍根方程,且x1=2,x2=-$\frac{n}{m}$,
∴$\frac{n}{m}$=-1,或$\frac{n}{m}$=-4,
∴m+n=0,4m+n=0,
∴4m2+5mn+n2=(4m+n)(m+n)=0;
(3)④∵方程ax2+bx+c=0是倍根方程,
∴设x1=2x2,
∵相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,
∴抛物线的对称轴x=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{1+t+4-t}{2}$=$\frac{5}{2}$,
∴x1+x2=5,
∴x2+2x2=5,
∴x2=$\frac{5}{3}$,
∴方程ax2+bx+c=0的一个根为$\frac{5}{3}$.
点评 本题考查了根与系数的关系,根的判别式,反比例函数图形上点的坐标特征,二次函数图形上点的坐标特征,正确的理解“倍根方程”的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
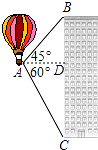 热气球的探测器显示,从热气球A看一栋楼顶部B的仰角α为45°,看这栋楼底部C的俯角β为60°,热气球与楼的水平距离为100m,求这栋楼的高度(结果保留根号).
热气球的探测器显示,从热气球A看一栋楼顶部B的仰角α为45°,看这栋楼底部C的俯角β为60°,热气球与楼的水平距离为100m,求这栋楼的高度(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
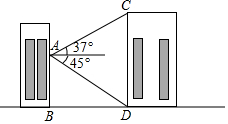 如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m)
如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
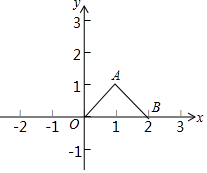 如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(1,1),在x轴上找出点B,使△AOB为等腰三角形,满足条件的点B的坐标为(1,0)或(-$\sqrt{2}$,0)或($\sqrt{2}$,0)或(2,0).
如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(1,1),在x轴上找出点B,使△AOB为等腰三角形,满足条件的点B的坐标为(1,0)或(-$\sqrt{2}$,0)或($\sqrt{2}$,0)或(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
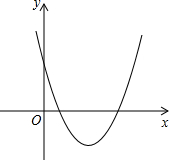 二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的图象经过( )
二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的图象经过( )| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,4) | B. | (-3,1) | C. | (0,-2) | D. | (3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com