
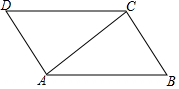
 如图,AC是平行四边形ABCD的对角线.
如图,AC是平行四边形ABCD的对角线.分析 (1)根据题意画出图形即可;
(2)由作图可知PQ是线段AC的垂直平分线,故可得出OA=OC,再由平行四边形的性质得出∠OCF=∠OAE,故可得出△OCF≌△OAE,据此可得出结论.
解答 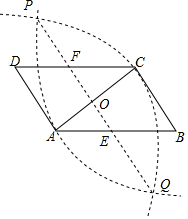 (1)解:如图;
(1)解:如图;
(2)证明:∵由作图可知,PQ是线段AC的垂直平分线,
∴OA=OC.
∵AB∥CD,
∴∠OCF=∠OAE.
在△OCF与△OAE中,
∵$\left\{\begin{array}{l}{∠OAE=∠OCF}\\{OC=OA}\\{∠COF=∠AOE}\end{array}\right.$,
∴△OCF≌△OAE(ASA),
∴AE=CF.
点评 本题考查的是作图-基本作图,熟知线段垂直平分线的作法是解答此题的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
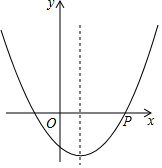 如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(5,0)在抛物线上,则9a-3b+c的值0.
如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(5,0)在抛物线上,则9a-3b+c的值0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
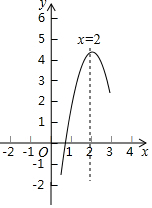 如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是x1=0.8,x2=3.2合理即可.(精确到0.1)
如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是x1=0.8,x2=3.2合理即可.(精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
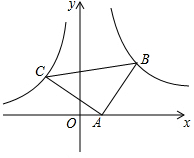 如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点C在双曲线y=-$\frac{4}{x}$(x<0)上,点A在x轴的正半轴上,且△ABC是以BC为斜边的等腰直角三角形.
如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点C在双曲线y=-$\frac{4}{x}$(x<0)上,点A在x轴的正半轴上,且△ABC是以BC为斜边的等腰直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 速度v(千米/小时) | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
| 流量q(辆/小时) | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
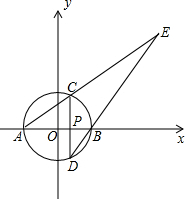 如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.
如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
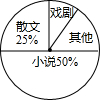 八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.| 类别 | 频数(人数) | 频率 |
| 小说 | 0.5 | |
| 戏剧 | 4 | |
| 散文 | 10 | 0.25 |
| 其他 | 6 | |
| 合计 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com