
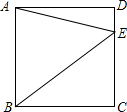
 如图,点E在正方形ABCD的边CD上,若△ABE的面积为8,DE=1,则线段BE=5.
如图,点E在正方形ABCD的边CD上,若△ABE的面积为8,DE=1,则线段BE=5. 分析 由S正方形ABCD=2S△ABE=16,先求出正方形的边长,再在RT△BCE中,利用勾股定理即可解决问题.
解答 解:∵四边形ABCD是正方形,
∴AB=CD=AD=BC,∠C=90°,
∵S正方形ABCD=2S△ABE=16,
∴AB=CD=BC=4,
∵DE=1,∴EC=3,
在RT△BCE中,∵∠C=90°,BC=4,EC=3,
∴BE=$\sqrt{B{C}^{2}+E{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
故答案为5.
点评 本题考查正方形的性质、勾股定理等知识,解题的关键是S正方形ABCD=2S△ABE的应用,记住这个结论,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
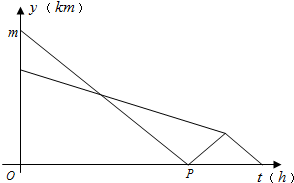 某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.
某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 气温x/℃ | 0 | 5 | 10 | 15 | 20 |
| 声速y/m•s-1 | 331 | 334 | 337 | 340 | 343 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
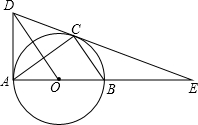 如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD.
如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
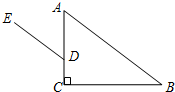 如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )
如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )| A. | 34° | B. | 54° | C. | 46° | D. | 44° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
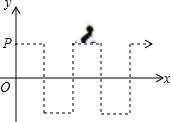 如图,在直角坐标系中,一只蚂蚁从点P(0,1)出发,沿着图示折线方向移动,第一次到达点(1,1),第二次达到点(1,0),第三次达到点(1,-1),第四次达到点(2,-1),…,按照这样的规律,第2016次到达点的坐标应为(672,1).
如图,在直角坐标系中,一只蚂蚁从点P(0,1)出发,沿着图示折线方向移动,第一次到达点(1,1),第二次达到点(1,0),第三次达到点(1,-1),第四次达到点(2,-1),…,按照这样的规律,第2016次到达点的坐标应为(672,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知实数a、b、c在数轴上的位置如图所示,a、b到原点的距离相等,化简:$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|
已知实数a、b、c在数轴上的位置如图所示,a、b到原点的距离相等,化简:$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|查看答案和解析>>
科目:初中数学 来源: 题型:选择题
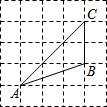 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com