(1)已知二次函数.请你化成的形式.并在直角坐标系中画出的图象,(2)如果.是(1)中图象上的两点.且.请直接写出.的大小关系,中的图象表示出方程的根来.要求保留画图痕迹.说明结果．题目和参考答案——青夏教育精英家教网—

（1）已知二次函数，请你化成的形式，并在直角坐标系中画出的图象；
（2）如果，是（1）中图象上的两点，且，请直接写出、的大小关系；
（3）利用（1）中的图象表示出方程的根来，要求保留画图痕迹，说明结果．

（1），图象见解析；（2）；（3）详见解析.

解析试题分析：（1）首先由“”想到应化为，此时比原来多了“1”，因此再减去1，据此将原函数解析式变形；画函数图象应确定几个基本点后，描点连线即可；（2）由图象可直接判断，得出结果；（3）由解析式可知将原图象向上平移两个单位即得到新的函数图象，其与x轴的交点即为所求的根.
试题解析：
解：（1）. 画图象，如图所示．

（2）．
（3）如图所示，将抛物线向上平移两个单位后得到抛物线，抛物线与x轴交于点A、B，则A、B两点的横坐标即为方程的根.
考点：二次函数的综合运用.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

如图,抛物线y=ax²+bx+c与x轴的一个交点A的坐标为（﹣1，0），对称轴为直线x=﹣2．

（1）求抛物线与x轴的另一个交点B的坐标；
（2）点D是抛物线与y轴的交点，点C是抛物线上的另一点．若以AB为一底边的梯形ABCD的面积为9．
求此抛物线的解析式，并指出顶点E的坐标；
（3）点P是（2）中抛物线对称轴上一动点，且以1个单位/秒的速度从此抛物线的顶点E向上运动．设点P运动的时间为t秒．
①当t为　　秒时，△PAD的周长最小？当t为秒时，△PAD是以AD为腰的等腰三角形？（结果保留根号）
②点P在运动过程中，是否存在一点P，使△PAD是以AD为斜边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

定义：把一个半圆与抛物线的一部分合成封闭图形，我们把这个封闭图形称为“蛋圆”．如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，A，B，C，D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0,8），AB为半圆的直径，半圆的圆心M的坐标为（1,0），半圆半径为3．

（1）请你直接写出“蛋圆”抛物线部分的解析式，自变量的取值范围是；
（2）请你求出过点C的“蛋圆”切线与x轴的交点坐标；
（3）求经过点D的“蛋圆”切线的解析式．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

一场篮球赛中,小明跳起投篮,已知球出手时离地面高米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,若篮球运行的轨迹为抛物线,篮圈中心距离地面3米.

（1）建立如图的平面直角坐标系,求抛物线的解析式；
（2）问此球能否投中？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为米,面积为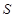平方米．（注：的近似值取3）

（1）求出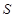与的函数关系式,并写出自变量的取值范围；
（2）当半径为何值时,扇形花坛的面积最大,并求面积的最大值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

二次函数的图象经过点，，．
（1）求此二次函数的关系式；
（2）求此二次函数图象的顶点坐标；
（3）填空：把二次函数的图象沿坐标轴方向最少平移个单位，使得该图象的顶点在原点．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

已知：如图，抛物线与y轴交于点C（0，4），与x轴交于点A、B，点A的坐标为（4，0）.

（1）求该抛物线的解析式；
（2）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ.当△CQE的面积最大时，求点Q的坐标；
（3）若平行于x轴的动直线与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）.问：是否存在这样的直线，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由.