
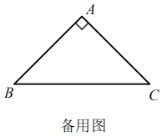
ЁОЬтФПЁПдкRtІЄABCжаЃЌЁЯBAC=90ЁуЃЌЕуOЪЧЁїABCЫљдкЦНУцФквЛЕуЃЌСЌНгOAЃЌбгГЄOAЕНЕуEЃЌЪЙЕУAE=OAЃЌСЌНгOCЃЌЙ§ЕуBзїBDгыOCЦНааЃЌВЂЪЙЁЯDBC=ЁЯOCBЃЌЧвBD=OCЃЌСЌНгDE.
(1)ШчЭМвЛЃЌЕБЕуOдкRtІЄABCФкВПЪБ.

ЂйАДЬтвтВЙШЋЭМаЮЃЛ
ЂкВТЯыDEгыBCЕФЪ§СПЙиЯЕЃЌВЂжЄУї.
(2)ШєAB=AC(ШчЭМЖў)ЃЌЧвЁЯOCB=30ЁуЃЌЁЯOBC=15ЁуЃЌЧѓЁЯAEDЕФДѓаЁ.


ЁОД№АИЁП(1)ЂйВЙШЋЭМаЮЃЌШчЭМвЛЃЌМћНтЮіЃЛЂкВТЯыDE=BC. жЄУїМћНтЮіЃЛ(2) ЁЯAED=30ЁуЛђ15Ёу.
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнвЊЧѓЛГіЭМаЮМДПЩНтОіЮЪЬтЃЎ
ЂкНсТлЃКDE=BCЃЎСЌНгODНЛBCгкFЃЌСЌНгAFЃЎжЄУїAFЮЊRtЁїABCаББпжаЯпЃЌЮЊЁїODEЕФжаЮЛЯпЃЌМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉЗжСНжжЧщаЮЃКШчЭМЖўжаЃЌЕБЕуOдкЁїABCФкВПЪБЃЌСЌНгODНЛBCгкFЃЌСЌНгAFЃЌбгГЄCOНЛAFгкMЃЎСЌНгBMЃЎжЄУїЁїBMAЁеЁїBMOЃЈAASЃЉЃЌЭЦГіAM=OMЃЌЁЯBMO=ЁЯBMA=120ЁуЃЌЭЦГіЁЯAMO=120ЁуЃЌМДПЩНтОіЮЪЬтЃЎШчЭМШ§жаЃЌЕБЕуOдкЁїABCЭтВПЪБЃЌЕБЕуOдкЁїABCФкВПЪБЃЌСЌНгODНЛBCгкFЃЌСЌНгAFЃЌбгГЄCOНЛAFгкMЃЎСЌНгBMЃЎЗжБ№ЧѓНтМДПЩЃЎ
(1)ЂйВЙШЋЭМаЮЃЌШчЭМвЛЃЌ

ЂкВТЯыDE=BC.
ШчЭМЃЌСЌНгODНЛBCгкЕуFЃЌСЌНгAF

дкЁїBDFКЭЁїCOFжаЃЌ

ЁрЁїBDFЁеІЄCOF
ЁрDF=OFЃЌBF=CF
ЁрFЗжБ№ЮЊBCКЭDOЕФжаЕу
ЁпЁЯBAC=90ЁуЃЌFЮЊBCЕФжаЕуЃЌ
ЁрAF=![]() BC.
BC.
ЁпOA=AEЃЌFЮЊBCЕФжаЕуЃЌ
ЁрAF=![]() ED.
ED.
ЁрDE=BC
ЃЈ2ЃЉШчЭМЖўжаЃЌЕБЕуOдкЁїABCФкВПЪБЃЌСЌНгODНЛBCгкFЃЌСЌНгAFЃЌбгГЄCOНЛAFгкMЃЎСЌНгBMЃЎ

гЩЃЈ1ЃЉПЩжЊЃКAFЮЊRtЁїABCаББпжаЯпЃЌЮЊЁїODEЕФжаЮЛЯпЃЌ
ЁпAB=ACЃЌ
ЁрAFДЙжБЦНЗжЯпЖЮBCЃЌ
ЁрMB=MCЃЌЁпЁЯOCB=30ЁуЃЌЁЯOBC=15ЁуЃЌ
ЁрЁЯMBC=ЁЯMCB=30ЁуЃЌ
ЁпЁЯBAC=90ЁуЃЌAB=ACЃЌ
ЁрЁЯABC=ЁЯACB=45ЁуЃЌЁЯMBO=ЁЯMBA=15ЁуЃЌ
ЁпЁЯBAM=ЁЯBOM=45ЁуЃЌBM=BMЃЌ
ЁрЁїBMAЁеЁїBMOЃЈAASЃЉЃЌ
ЁрAM=OMЃЌЁЯBMO=ЁЯBMA=120ЁуЃЌ
ЁрЁЯAMO=120ЁуЃЌ
ЁрЁЯMAO=ЁЯMOA=30ЁуЃЌ
ЁрЁЯAED=ЁЯMAO=30ЁуЃЎ
ШчЭМШ§жаЃЌЕБЕуOдкЁїABCЭтВПЪБЃЌЕБЕуOдкЁїABCФкВПЪБЃЌСЌНгODНЛBCгкFЃЌСЌНгAFЃЌбгГЄCOНЛAFгкMЃЎСЌНгBMЃЎ

гЩЁЯBOM=ЁЯBAM=45ЁуЃЌПЩжЊAЃЌBЃЌMЃЌOЫФЕуЙВдВЃЌ
ЁрЁЯMAO=ЁЯMBO=30Ёу-15Ёу=15ЁуЃЌ
ЁпDEЁЮAMЃЌ
ЁрЁЯAED=ЁЯMAO=15ЁуЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЁЯAEDЕФжЕЮЊ15ЁуЛђ30ЁуЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,вбжЊЫФБпаЮABCDжа,ЁЯB=90Ёу,AB=3,BC=4,CD=12,AD=13,ЧѓЫФБпаЮABCDЕФУцЛ§ЮЊ______ЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЁЯABCКЭЁЯACBЕФЦНЗжЯпНЛгкЕуO.
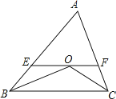
(1) НсКЯЭМаЮЃЌЧыФуаДГіФуШЯЮЊе§ШЗЕФНсТлЃЛ
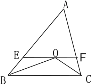
(2) Й§OзїEFЁЮBCНЛABгкEЃЌНЛACгкF. ЧыФуаДГіЭМжаЫљгаЕШбќШ§НЧаЮЃЌВЂЬНОПEFЁЂBEЁЂFCжЎМфЕФЙиЯЕЃЛ

(3) ШєABЁйACЃЌЦфЫћЬѕМўВЛБфЃЌЭМжаЛЙгаЕШбќШ§НЧаЮТ№ЃПШєгаЃЌЧыаДГіЫљгаЕФЕШбќШ§НЧаЮЃЌШєУЛгаЃЌЧыЫЕУїРэгЩЃЛЯпЖЮEFЁЂBEЁЂFCжЎМфЃЌЩЯУцЬНОПЕФНсТлЪЧЗёЛЙГЩСЂЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЫЎЦНЗХжУвЛИіШ§НЧАхКЭвЛИіСПНЧЦїЃЌШ§НЧАхЕФБпABКЭСПНЧЦїЕФжБОЖDEдквЛЬѕжБЯпЩЯЃЌЁЯACB=90ЁуЃЌЁЯBAC=30ЁуЃЌOD=3cmЃЌПЊЪМЕФЪБКђBD=1cmЃЌЯждкШ§НЧАхвд2cm/sЕФЫйЖШЯђгввЦЖЏЃЎ
ЃЈ1ЃЉЕБЕуBгкЕуOжиКЯЕФЪБКђЃЌЧѓШ§НЧАхдЫЖЏЕФЪБМфЃЛ
ЃЈ2ЃЉШ§НЧАхМЬајЯђгвдЫЖЏЃЌЕБBЕуКЭEЕужиКЯЪБЃЌACгыАыдВЯрЧагкЕуFЃЌСЌНгEFЃЌШчЭМ2ЫљЪОЃЎ
ЂйЧѓжЄЃКEFЦНЗжЁЯAECЃЛ
ЂкЧѓEFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЯТСаЩњЛюЁЂЩњВњЯжЯѓжаЃЌПЩвдгУЛљБОЪТЪЕЁАСНЕуШЗЖЈвЛЬѕжБЯпЁБРДНтЪЭЕФЪЧЃЈЁЁЁЁЃЉ
ЂйгУСНПХЖЄзгОЭПЩвдАбФОЬѕЙЬЖЈдкЧНЩЯЃЛЂкАбБЪМтПДГЩвЛИіЕуЃЌЕБетИіЕудЫЖЏЪББуЕУЕНвЛЬѕЯпЃЛЂлАбЭфЧњЕФЙЋТЗИФжБЃЌОЭФмЫѕЖЬТЗГЬЃЛЂмжВЪїЪБЃЌжЛвЊддЯТСНПУЪїЃЌОЭПЩвдАбЭЌвЛааЪїдддкЭЌвЛЬѕжБЯпЩЯЃЎ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП10ИіШЫЮЇГЩвЛШІзігЮЯЗ.гЮЯЗЕФЙцдђЪЧЃКУПИіШЫаФРяЖМЯывЛИіЪ§ЃЌВЂАбФПМКЯыЕФЪ§ИцЫпгыЫћЯрСкЕФСНИіШЫЃЌШЛКѓУПИіШЫНЋгыЫћЯрСкЕФСНИіШЫИцЫпЫћЕФЪ§ЕФЦНОљЪ§БЈГіРДЃЌШєБЈГіРДЕФЪ§ШчЭМЫљЪОЃЌдђБЈГіРДЕФЪ§ЪЧ3ЕФШЫаФРяЯыЕФЪ§ЪЧЃЈ ЃЉ

A.2B.![]() C.4D.
C.4D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШє![]() ЃЌдђвдЯТЫФИіНсТлжаЃЌе§ШЗЕФЪЧЃЈ ЃЉ
ЃЌдђвдЯТЫФИіНсТлжаЃЌе§ШЗЕФЪЧЃЈ ЃЉ
A.![]() вЛЖЈЪЧе§Ъ§B.
вЛЖЈЪЧе§Ъ§B.![]() ПЩФмЪЧИКЪ§
ПЩФмЪЧИКЪ§
C.![]() вЛЖЈЪЧе§Ъ§D.
вЛЖЈЪЧе§Ъ§D.![]() вЛЖЈЪЧе§Ъ§
вЛЖЈЪЧе§Ъ§
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЌBЕФзјБъЗжБ№ЮЊЃЈЉ1ЃЌ0ЃЉЃЌЃЈ3ЃЌ0ЃЉЃЌНЋЯпЖЮABЯШЯђЩЯЦНвЦ2ИіЕЅЮЛГЄЖШЃЌдйЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНЯпЖЮCDЃЌСЌНгACЃЌBDЃЌЙЙГЩЦНааЫФБпаЮABDCЃЎ
ЃЈ1ЃЉЧыаДГіЕуCЕФзјБъЮЊЁЁ ЁЁЃЌЕуDЕФзјБъЮЊЁЁ ЁЁЃЌSЫФБпаЮABDCЁЁ ЁЁЃЛ
ЃЈ2ЃЉЕуQдкyжсЩЯЃЌЧвSЁїQABЃНSЫФБпаЮABDCЃЌЧѓГіЕуQЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЃЈ2ЃЉЃЌЕуPЪЧЯпЖЮBDЩЯШЮвтвЛИіЕуЃЈВЛгыBЁЂDжиКЯЃЉЃЌСЌНгPCЁЂPOЃЌЪдЬНЫїЁЯDCPЁЂЁЯCPOЁЂЁЯBOPжЎМфЕФЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжАвЕИпжаЛњЕчАрЙВгабЇЩњ42ШЫЃЌЦфжаФаЩњШЫЪ§БШХЎЩњШЫЪ§ЕФ2БЖЩй3ШЫЃЎ
ЃЈ1ЃЉИУАрФаЩњКЭХЎЩњИїгаЖрЩйШЫЃП
ЃЈ2ЃЉФГЙЄГЇОіЖЈЕНИУАреаТМ30УћбЇЩњЃЌОВтЪдЃЌИУАрФаЁЂХЎЩњУПЬьФмМгЙЄЕФСуМўЪ§ЗжБ№ЮЊ50ИіКЭ45ИіЃЌЮЊБЃжЄЫћУЧУПЬьМгЙЄЕФСуМўзмЪ§ВЛЩйгк1460ИіЃЌФЧУДжСЩйвЊеаТМЖрЩйУћФабЇЩњЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com