
分析 (1)根据题目给出的方法即可直接写出答案;
(2)先求出8条直线两两相交时的交点个数,再写出4条直线两两相交时的个数,作差即可得解;
(3)把9条公路看作是9条直线,先求出9条直线两两相交时的交点的个数,再根据差是12进行分析,即可得解.
解答 解:(1)$\frac{n(n-1)}{2}$;
(2)=$\frac{8×7}{2}$-$\frac{4×3}{2}$=28-6=22;
(3)把9条公路看作是9条直线,则9条公路两两相交时交点的个数为:$\frac{9×8}{2}$=36,
36-24=12,
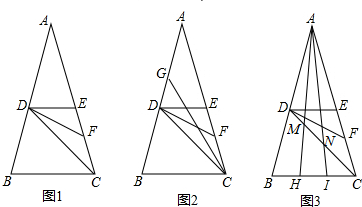
①12=10+1+1,则可以看作,有5条直线两两互相平行,其余4条直线不平行,但每两条互相平行,如图: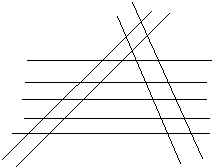
②12=6+6,即有4条直线分别平行,另4条直线分别平行,但这两组直线不平行,如图: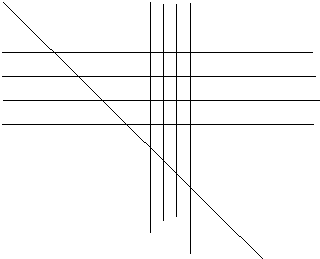
点评 本题主要考查了学生的阅读理解能力,以及学生的自学能力,读懂题意是解题的关键,还考查了学生动手操作以及分类讨论的能力,是比较难的题目,要注意总结.


科目:初中数学 来源: 题型:填空题
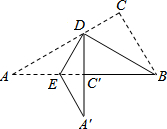 如图,在Rt△ABC中,∠ACB=90°,将△ABC沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,再将其沿DE折叠,使点A落在DC′的延长线上的A′处.若△BED与△ABC相似,则相似比$\frac{BD}{AC}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠ACB=90°,将△ABC沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,再将其沿DE折叠,使点A落在DC′的延长线上的A′处.若△BED与△ABC相似,则相似比$\frac{BD}{AC}$=$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y是x的一次函数 | B. | y是x的正比例函数 | ||
| C. | y是x的函数但不是正比例函数 | D. | y不是x的函数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.2×10-6cm | B. | 2×10-6cm | C. | 0.2×10-7cm | D. | 2×10-7cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com