
如图,在梯形 ABCD中,AD∥BC,∠B=90º,AD=8cm,AB=6 cm,BC=10 cm,点Q从点A出发以1 cm/s的速度向点D运动,点P从点B出发以2cm/s的速度在线段BC间往返运动,P、Q两点同时出发,当点Q到达点D时,两点同时停止运动。

⑴当t= s时,四边形PCDQ的面积为36 ;
;
⑵若以P、Q、C、D为顶点的四边形是平行四边形,求t的值;
⑶ 当0<t<5时,若DQ≠DP,当 t 为何值时,△DPQ是等腰三角形 .
(1)t=2;(2)
t=2或t=6;(3)t= 或
或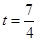
【解析】
试题分析:(1)由题意可知,四边形PCDQ为梯形,先分别表示出上底和下底,再根据梯形的面积公式列方程求解;
(2)分情况讨论:①P未到达C点时;②P到达C点并返回时,根据平行四边形的对边相等列方程求解即可;
(3) ①若PQ=PD,过P作PE⊥AD于E,则QD=8-t,即可表示出QE、AE,再根据AE=BP即可求得结果;②若QD=QP,过Q作QF⊥BC于F,则QF=6,
FP=2t-t=t,在Rt△QPF中,根据勾股定理得: ,即可求得结果。
,即可求得结果。
(1)t=2
(2)①P未到达C点时,8-t=10-2t,t=2
②P到达C点并返回时,8-t=2t-10,t=6
(3) ①如图,若PQ=PD,过P作PE⊥AD于E,
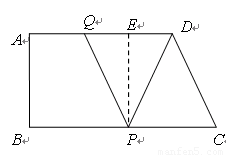
则QD=8-t,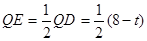
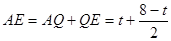
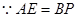

∴ t=
② 如图,若QD=QP,过Q作QF⊥BC于F,
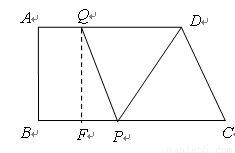
则QF=6,FP=2t-t=t
在Rt△QPF中,由勾股定理得:

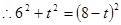
∴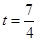
∴当t= 或
或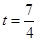 时,△DPQ是等腰三角形.
时,△DPQ是等腰三角形.
考点:本题考查的是梯形的性质,平行四边形的性质,勾股定理,等腰三角形的性质
点评:解答本题的关键是掌握梯形的面积公式,平行四边形的对边相等的性质,等腰三角形的腰相等的性质。


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:初中数学 来源: 题型:
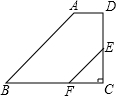 如图,在梯形ABCD中,AD∥BC,∠C=90°,E为CD的中点,EF∥AB交BC于点F
如图,在梯形ABCD中,AD∥BC,∠C=90°,E为CD的中点,EF∥AB交BC于点F查看答案和解析>>
科目:初中数学 来源: 题型:
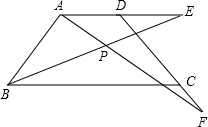 延长线上,且DE=CF.AF交BE于P.
延长线上,且DE=CF.AF交BE于P.查看答案和解析>>
科目:初中数学 来源: 题型:
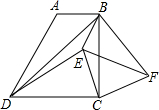 如图,在梯形ABCD中,AB∥CD,∠BCD=90°,BD平分∠ABC.
如图,在梯形ABCD中,AB∥CD,∠BCD=90°,BD平分∠ABC.| BE | BF |
查看答案和解析>>
科目:初中数学 来源:1+1轻巧夺冠·优化训练·八年级数学下 题型:013
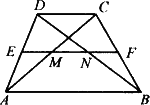
如图,在梯形ABC中,AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18 cm,MN=8 cm,则AB的长等于
A.10 cm
B.13 cm
C.20 cm
D.26 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com