
【题目】如图,一艘快艇从O港出发,向西北方向行驶到M处,然后向正东行驶到N处,再向西南方向行驶,共经过1.5小时回到O港,已知快艇的速度是每小时50海里,则M,N之间的距离是( )海里

A.75![]() ﹣75B.
﹣75B.![]() C.75
C.75![]() D.50
D.50![]()
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
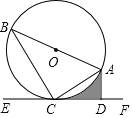
【题目】如图,⊙O是Rt△ABC的外接圆,直径AB=4,直线EF经过点C,AD⊥EF于点D,∠ACD=∠B.
(1)求证:EF是⊙O的切线;
(2)若AD=1,求BC的长;
(3)在(2)的条件下,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校1200名学生参加了“垃圾分类知识竞赛”,为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.
(1)学校设计了以下三种抽样调查方案:
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
其中抽取的样本具有代表性的方案是__________.(填“方案一”、“方案二”或“方案三”)
(2)学校根据样本数据,绘制成下表(90分及以上为“优秀”,60分及以上为“及格”):
样本容量 | 平均分 | 及格率 | 优秀率 | 最高分 | 最低分 |
100 | 93.5 |
|
| 100 | 80 |
分数段统计(学生成绩记为 | |||||
分数段 |
|
|
|
|
|
频数 | 0 | 5 | 25 | 30 | 40 |
请结合表中信息解答下列问题:
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;
②估计该校1200名学生中达到“优秀”的学生总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地之间有一条笔直的公路,小明从甲地出发步行前往乙地,同时小亮从乙地出发骑自行车前往甲地,小亮到达甲地没有停留,按原路原速返回,追上小明后两人一起步行到乙地.如图,线段OA表示小明与甲地的距离y1(米)与行走的时间x(分钟)之间的函数关系:折线BCDA表示小亮与甲地的距离y2(米)与行走的时间x(分钟)之间的函数关系.请根据图象解答下列问题:
(1)小明步行的速度是 米/分钟,小亮骑自行车的速度是 米/分钟;
(2)线段OA与BC相交于点E,求点E坐标;
(3)请直接写出小亮从乙地出发到追上小明的过程中,与小明相距100米时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
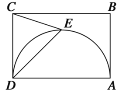
【题目】如图,在矩形ABCD中,AD=6,AB=4,以AD为直径在矩形内作半圆,点E为半圆上的一动点(不与A、D重合),连接DE、CE,当△DEC为等腰三角形时,DE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com