
【题目】已知二次函数y=ax+bx+c(a≠0)的图象如图所示,以下结论中正确的个数是( )
①abc>0、②3a>2b、③m(am+b)≤a﹣b(m为任意实数)、④4a﹣2b+c<0.
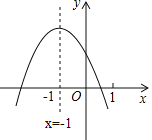
A.1B.2C.3D.4
【答案】C
【解析】
由抛物线开口向下得a<0,由抛物线的对称轴为直线x=﹣![]() =﹣1得b=2a<0,由抛物线与y轴的交点在x轴上方得c>0,所以abc>0;由b=2a,则2b﹣3a=a<0,所以2b<3a;根据抛物线的对称轴为直线x=﹣1,开口向下,得到当x=﹣1时,y有最大值,所以am2+bm+c≤a﹣b+c(m为任意实数),整理得到m(am+b)≤a﹣b(m为任意实数);根据抛物线的对称性得到抛物线与x轴的一个交点在点(﹣3,0)和(﹣2,0)之间,则当x=﹣2时,y>0,即4a﹣2b+c>0.
=﹣1得b=2a<0,由抛物线与y轴的交点在x轴上方得c>0,所以abc>0;由b=2a,则2b﹣3a=a<0,所以2b<3a;根据抛物线的对称轴为直线x=﹣1,开口向下,得到当x=﹣1时,y有最大值,所以am2+bm+c≤a﹣b+c(m为任意实数),整理得到m(am+b)≤a﹣b(m为任意实数);根据抛物线的对称性得到抛物线与x轴的一个交点在点(﹣3,0)和(﹣2,0)之间,则当x=﹣2时,y>0,即4a﹣2b+c>0.
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=﹣![]() =﹣1<0,
=﹣1<0,
∴b=2a,
∴b<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc>0,所以①正确;
∵b=2a,
∴3a﹣2b=3a﹣4a=﹣a>0,
∴3a>2b,所以②正确;
∵抛物线的对称轴为直线x=﹣1,
∴当x=﹣1时,y有最大值,
∴am2+bm+c≤a﹣b+c(m为任意实数),
∴m(am+b)≤a﹣b(m为任意实数),所以③正确;
∵抛物线的对称轴为直线x=﹣1,抛物线与x轴的一个交点在点(0,0)和(1,0)之间,
∴抛物线与x轴的一个交点在点(﹣3,0)和(﹣2,0)之间,
∴当x=﹣2时,y>0,
∴4a﹣2b+c>0,所以④错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7

(1)指出旋转中心和旋转角度.
(2)求DE的长度.
(3)BE与DF垂直吗? 说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 纸片中,
纸片中,![]() ,
,![]() ,
,![]() .如图,直角顶点
.如图,直角顶点![]() 在原点,点
在原点,点![]() 在
在![]() 轴负半轴上,当点
轴负半轴上,当点![]() 在
在![]() 轴上向上移动时,点
轴上向上移动时,点![]() 也随之在
也随之在![]() 轴上向右移动,当点
轴上向右移动,当点![]() 到达原点时,点
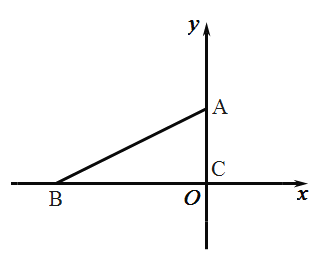
到达原点时,点![]() 停止移动.在移动过程中,点
停止移动.在移动过程中,点![]() 到原点的最大距离是__________.
到原点的最大距离是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2(a≠0).
(1)该二次函数图象的对称轴是直线 ;
(2)若该二次函数的图象开口向上,当﹣1≤x≤5时,函数图象的最高点为M,最低点为N,点M的纵坐标为![]() ,求点M和点N的坐标;
,求点M和点N的坐标;
(3)若该二次函数的图象开口向下,对于该二次函数图象上的两点A(x1,y1)、B(x2,y2),当x2≥3时,均有y1≥y2,请结合图象,直接写出x1的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,D是弧BC的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.
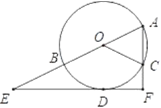
(1)求证:EF是⊙O的切线;
(2)若AF=6,EF=8,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com