
分析 分析:利用因式分解法分解方程,得出方程的根,根据整数根得出符合要求的根
解答 解:解:原方程可化为[(m-6)x+9][(x-9)x+6]=0,
解得 x1=$\frac{9}{6-m}$,${x}_{2}=\frac{6}{9-m}$,
要使x1为整数,必须 6-m=-9、-3、-1、1、3、9,即 m=-3、3、5、7、9、15;
要使x2为整数,必须 9-m=-6、-3、-2、-1、1、2、3、6,即 m=3、6、7、8、10、11、12、15;
而 x1、x2均为整数,所以 m=3 或6或115,
当m=6或9时,此方程是一元一次方程,原方程有整数根,
所以,当 m=3 或 m=7 或 m=15或m=6或m=9 时,原方程只有整数根.
点评 此题主要考查了十字相乘法解方程,以及求方程整数根,题目难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=140}\\{16x+6y=15}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=15}\\{16x+6y=140}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=140}\\{6x+16y=15}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=15}\\{6x+16y=140}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
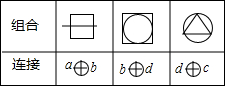 字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形
字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形 的连接方式为a⊕c.
的连接方式为a⊕c.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com