
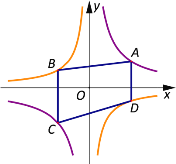
【题目】如图,已知点A、C在双曲线![]() 上,点 B、D在双曲线
上,点 B、D在双曲线![]() 上,AD// BC//y 轴.
上,AD// BC//y 轴.
(I)当m=6,n=-3,AD=3 时,求此时点 A 的坐标;
(II)若点A、C关于原点O对称,试判断四边形 ABCD的形状,并说明理由;
(III)若AD=3,BC=4,梯形ABCD的面积为![]() ,求mn 的最小值.
,求mn 的最小值.

【答案】(I) 点![]() 的坐标为
的坐标为![]() ;(II) 四边形
;(II) 四边形![]() 是平行四边形,理由见解析;(III)
是平行四边形,理由见解析;(III) ![]() 的最小值是
的最小值是![]() .
.
【解析】
(I)由![]() ,
,![]() ,可得
,可得![]() ,
,![]() .分别表示出点A、D的坐标,根据
.分别表示出点A、D的坐标,根据![]() ,即可求出点A的坐标.
,即可求出点A的坐标.
(II)根据点A、C关于原点O对称,设点A的坐标为:![]() ,即可分别表示出B、C、D的坐标,然后可得出
,即可分别表示出B、C、D的坐标,然后可得出![]() 与
与![]() 互相平分可证明出四边形
互相平分可证明出四边形![]() 是平行四边形.
是平行四边形.
(III) 设![]() 与
与![]() 的距离为
的距离为![]() ,由
,由![]() ,
,![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,可求出h=7,根据
,可求出h=7,根据![]() ,
,![]() ,可得
,可得![]() ,进而得出答案.
,进而得出答案.
(I) ∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
由![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∴此时点![]() 的坐标为
的坐标为![]() .
.
(II)四边形![]() 是平行四边形,理由如下:
是平行四边形,理由如下:
设点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 、
、![]() 关于原点
关于原点![]() 对称,∴点
对称,∴点![]() 的坐标为
的坐标为![]() ,
,
∵![]() ∥
∥![]() ∥
∥![]() 轴,且点
轴,且点![]() 、
、![]() 在双曲线
在双曲线![]() 上,
上,![]()
![]() ,
,
∴点![]()
![]() ,点
,点![]()
![]() ,
,
∴点B与点D关于原点O对称,即![]() ,且
,且![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
又点![]() 、C关于原点O对称,即
、C关于原点O对称,即![]() ,且
,且![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
∴![]() 与
与![]() 互相平分.
互相平分.
∴四边形![]() 是平行四边形.
是平行四边形.
(III)设![]() 与
与![]() 的距离为
的距离为![]() ,
,![]() ,
,![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() ,
,![]() ,
,![]() ,
,
由![]() ,
,![]() ,可得:
,可得: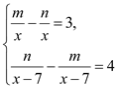 ,
,
则![]() ,
,![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,
∵![]() .
.
∴![]() .
.
∴![]() ,即
,即![]() .
.
又![]() ,
,![]() ,
,
∴当![]() 取到等号 .
取到等号 .
即![]() ,
,![]() 时,
时, ![]() 的最小值是
的最小值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,且AB=8,DB=2. 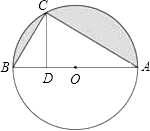
(1)求证:△ABC∽△ACD;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年来,国家对购买新能源汽车实行补助政策,2016年某省对新能源汽车中的“插电式混合动力汽车”实行每辆3万元的补助,小刘对该省2016年“纯电动乘用车”和“插电式混合动力车”的销售计划进行了研究,绘制出如图所示的两幅不完整的统计图.
(1)补全条形统计图;
(2)求出“D”所在扇形的圆心角的度数;
(3)为进一步落实该政策,该省计划再补助4.5千万元用于推广上述两大类产品,请你预测,该省16年计划大约共销售“插电式混合动力汽车”多少辆?
注:R为纯电动续航行驶里程,图中A表示“纯电动乘用车”(100km≤R<150km),B表示“纯电动乘用车”(150km≤R<250km),C表示“纯电动乘用车”(R≥250km),D为“插电式混合动力汽车”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与直线
与直线![]() 相交于点 A .
相交于点 A .
(I)求直线![]() 与 x 轴的交点坐标,并在坐标系中标出点 A 及画出直线
与 x 轴的交点坐标,并在坐标系中标出点 A 及画出直线 ![]() 的图象;
的图象;
(II)若点P是直线![]() 在第一象限内的一点,过点P作 PQ//y 轴交直线
在第一象限内的一点,过点P作 PQ//y 轴交直线 ![]() 于点Q,△POQ 的面积等于60 ,试求点P 的横坐标.
于点Q,△POQ 的面积等于60 ,试求点P 的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]() ,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( ) 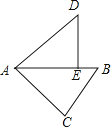
A.![]()
B.2 ![]()
C.3
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子有:①90°﹣∠β;②∠α﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β),其中错误的有( )个
(∠α﹣∠β),其中错误的有( )个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(﹣2,3),先把△ABC向右平移4个单位得到△A1B1C1 , 再作△A1B1C1关于x轴对称图形△A2B2C2 , 则顶点A2的坐标是________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com