
分析 (1)由四位数$\overline{123k}$是一个“精巧数”,可得1230+k是4的倍数;即可得1230+k=4n,继而可求得答案;
(2)由$\overline{2ab}$是“精巧数”,可得a为偶数,且2+a+b是3的倍数,且2+a+b<30,又由$\overline{2ab}$各位数字之和为一个完全平方数,可得2+a+b=32=9,继而求得答案.
解答 解:(1)∵四位数$\overline{123k}$是一个“精巧数”,
∴1230+k是4的倍数;
即1230+k=4n,
当n=308时,k=2;
当n=309时,k=6,
∴k=2或6;
(2)∵$\overline{2ab}$是“精巧数”,
∴a为偶数,且2+a+b是3的倍数,
∵a<10,b<10,
∴2+a+b<30,
∵$\overline{2ab}$各位数字之和为一个完全平方数,
∴2+a+b=32=9,
∴当a=0时,b=7,
当a=2时,b=5,
当a=4时,b=3,
当a=6时,b=1,
∴所有满足条件的三位“精巧数”有:207,225,243,261.
点评 此题考查了完全平方数的应用问题.注意掌握数的整除问题,注意掌握分类讨论思想的应用是解此题的关键.


科目:初中数学 来源: 题型:解答题
 证明“三角形的外角和等于360°”.
证明“三角形的外角和等于360°”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
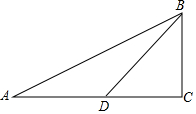 在Rt△ABC中,∠ACB=90°,D是AC上一点,∠A=α,∠ABD=β,若tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,求:tan(α+β)的值.
在Rt△ABC中,∠ACB=90°,D是AC上一点,∠A=α,∠ABD=β,若tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,求:tan(α+β)的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 第503个正方形的左下角 | B. | 第503个正方形的右下角 | ||
| C. | 第504个正方形的左下角 | D. | 第504个正方形的右上角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | MA=MB,NA=NB | B. | MA=MB,MN⊥AB | C. | MA=NA,MB=NB | D. | MA=MB,MN平分AB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7、24、25 | B. | $\frac{3}{4}$,1,$\frac{5}{4}$ | C. | 9、40、42 | D. | 12、15、20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com