
【题目】(1)有理数![]() 在数轴上的位置如图所示,且
在数轴上的位置如图所示,且![]() ,化简:
,化简:![]() .
.
![]()
(2).已知![]() 在数轴上的位置如图所示,化简:
在数轴上的位置如图所示,化简:![]() .
.
![]()
【答案】(1)b﹣a;(2)﹣a+c-b+1.
【解析】
(1)由数轴可知:b>c>0,a<0,a+b=0,再根据有理数的运算法则,求出绝对值里的代数式的正负性,最后根据绝对值的性质化简.
(2)先根据数轴上各点的位置确定2a、a+c、1﹣b的符号,再根据绝对值的性质去掉绝对值符号,合并同类项即可.
(1)由数轴,得b>c>0,a<0,又|a|=|b|,∴c﹣a>0,c﹣b<0,a+b=0.
|c﹣a|+|c﹣b|+|a+b|=c﹣a+b﹣c=b﹣a.
(2)∵a、c在原点的左侧,∴a<0,c<0,∴2a<0,a+c<0.
∵0<b<1,∴1﹣b>0,∴原式=﹣2a+(a+c)+1﹣b=﹣2a+a+c+1﹣b=﹣a+c-b+1.


科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴、y轴分别相交于点A(﹣1,0)、B(0,3)两点,其顶点为D. 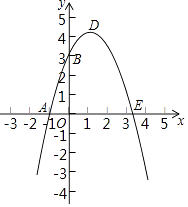
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出P点的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 36=15+21 B. 25=9+16 C. 13=3+10 D. 49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村计划对总长为1800m的道路进行改造,安排甲、乙两个工程队完成.已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成道路的长度分别是多少m?
(2)若村委每天需付给甲队的道路改造费用为0.4万元,乙队为0.25万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,∠ABC=∠BEF=60°,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC,探究PG与PC的位置关系。
(1)请你写出上面问题中线段PG与PC的位置关系,并说明理由;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明,
(3)将菱形ABCD和菱形BEFG均改成正方形,如图3,P为DF的中点,此时PG与PC的位置关系和数量关系分别是什么?直接写出答案。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线y=ax2+bx+c与x轴交于A(x1,0)、B(x2,0)两点(x1<0<x2),与y轴交于点C(0,-3),若抛物线的对称轴为直线x=1,且tan∠OAC=3.
(1)求抛物线的函数解析式;
(2)若点D是抛物线BC段上的动点,且点D到直线BC距离为 ![]() ,求点D的坐标
,求点D的坐标
(3)如图(2),若直线y=mx+n经过点A,交y轴于点E(0, - ![]() ),点P是直线AE下方抛物线上一点,过点P作x轴的垂线交直线AE于点M,点N在线段AM延长线上,且PM=PN,是否存在点P,使△PMN的周长有最大值?若存在,求出点P的坐标及△PMN的周长的最大值;若不存在,请说明理由.
),点P是直线AE下方抛物线上一点,过点P作x轴的垂线交直线AE于点M,点N在线段AM延长线上,且PM=PN,是否存在点P,使△PMN的周长有最大值?若存在,求出点P的坐标及△PMN的周长的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com