
【题目】如图,点O为线段AD外一点,M、C、B、N为AD上任意四点,连接OM、OC、OB、ON,下列结论不正确的是( )
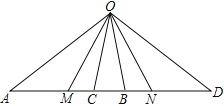
A. 以O为顶点的角共有15个
B. 若OM平分∠AOC,ON平分∠BOD,∠AOD=5∠COB,则∠MON=![]() (∠MOC+∠BON)
(∠MOC+∠BON)
C. 若M为AB中点,N为CD中点,则MN=![]() (AD-CB)
(AD-CB)
D. 若MC=CB,MN=ND,则CD=2CN
【答案】D
【解析】
A.以O为顶点的角的射线一共有6条射线,所以角的个数为6×(6-1)÷2=15个角,由此得出答案即可;
B.根据角平分线的定义和角的和差即可得到结论,根据已知条件列方程即可得到结论;
C. 根据线段的和差,可得MN=MB-CB+CN,根据线段中点的性质,可得MB,CB,CN的关系,再根据线段的和差,可得答案;
D. 由中点可得线段相等,进而可得出线段之间的数量关系.
解:A.6×(6-1)÷2=15个角,故正确;
B. ∵∠AOD=5∠COB,
∴设∠COB=x°,则∠AOD=5x°,
∴∠AOC+∠BOD=5x°- x°=4x°,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC+∠BON=2x°,
∴∠MON=2x°+ x°=3 x°,
∴∠MON=![]() (∠MOC+∠BON),
(∠MOC+∠BON),
故正确;
C. ∵M为AB中点,N为CD中点,
∴MB=![]() AB,CN=
AB,CN=![]() CD,
CD,
∴MN=MB-CB+CN
=![]() AB-CB+
AB-CB+![]() CD
CD
=![]() (AB+CD)-CB
(AB+CD)-CB
=![]() (AD+CB-2CD)
(AD+CB-2CD)
=![]() (AD-CB),
(AD-CB),
故正确;
D. ∵MC=CB,MN=ND
∴CD=MD-MC=2MN-![]() MC,
MC,
得不出CD=2CN,
故错误,
故选D.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+ ![]() x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC.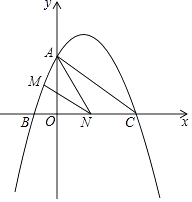
(1)请直接写出二次函数y=ax2+ ![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时N的坐标.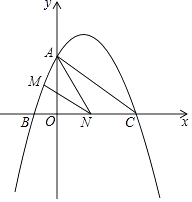
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的⊙O过点E. 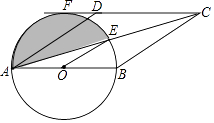
(1)求证:四边形ABCD的是菱形;
(2)若CD的延长线与圆相切于点F,已知直径AB=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=x+6,下列结论错误的是( )
A. 函数图象与x轴交点坐标是(0,6) B. 函数值随自变量的增大而增大
C. 函数图象与x轴正方向成45°角 D. 函数图象不经过第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: ![]() .我们称使得
.我们称使得![]() 成立的一对数
成立的一对数![]() ,
, ![]() 为“相伴数对”,记为
为“相伴数对”,记为![]() .
.
(1)若![]() 是“相伴数对”,求
是“相伴数对”,求![]() 的值;
的值;
(2)写出一个“相伴数对” ![]() ,其中
,其中![]() 且
且![]() ;
;
(3)若![]() 是“相伴数对”,求代数式
是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
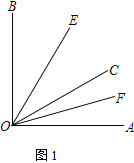
【题目】已知∠AOB内部有3条射线OE、OC、OF
(1) 如图1,若∠AOB = 90°,∠AOC = 30°,OE平分∠BOC,OF平分∠AOC,求∠EOF的度数.
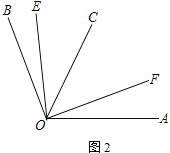
(2) 如图2,若∠AOB = α,∠EOB = ∠COB,∠COF = ∠FOA,求∠EOF的度数(用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,AB=AC=10,BC=12,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,直线![]() 分别交x、y轴于点A、C,点B在x轴负半轴上,过点A作
分别交x、y轴于点A、C,点B在x轴负半轴上,过点A作![]() 于点K,若
于点K,若![]() ,
,![]() .
.
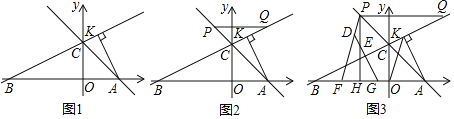
![]() 如图1,求点B坐标;
如图1,求点B坐标;
![]() 如图2,点P为AC延长线上一点,过点P作
如图2,点P为AC延长线上一点,过点P作![]() 交直线BC于点Q,设点P的横坐标为t,PQ长为d,求d与t的函数关系式
交直线BC于点Q,设点P的横坐标为t,PQ长为d,求d与t的函数关系式![]() 不必写出自变量t的取值范围
不必写出自变量t的取值范围![]() ;
;
![]() 在
在![]() 的条件下,连接OK,过点P作
的条件下,连接OK,过点P作![]() 轴于点H,点F为HB上一点,连接PF,点D在PF上,将点F沿x轴正方向平移
轴于点H,点F为HB上一点,连接PF,点D在PF上,将点F沿x轴正方向平移![]() 个单位到点G,连接DG,交PH于点E,若
个单位到点G,连接DG,交PH于点E,若![]() ,
,![]() ,
,![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com