
【题目】![]() 是等边三角形,点P在
是等边三角形,点P在![]() 的延长线上,以P为中心,将线段
的延长线上,以P为中心,将线段![]() 逆时针旋转n°(
逆时针旋转n°(![]() )得线段
)得线段![]() ,连接
,连接![]() ,
,![]() .
.


(1)如图,若![]() ,画出当
,画出当![]() 时的图形,并写出此时n的值;
时的图形,并写出此时n的值;
(2)M为线段![]() 的中点,连接
的中点,连接![]() .写出一个n的值,使得对于
.写出一个n的值,使得对于![]() 延长线上任意一点P,总有
延长线上任意一点P,总有![]() ,并说明理由.
,并说明理由.
【答案】(1)60°;(2)n=120°,理由见详解.
【解析】
(1)由![]() 是等边三角形,得∠BAC=∠ACB=60°,由
是等边三角形,得∠BAC=∠ACB=60°,由![]() ,
,![]() ,得∠PBQ=∠CPA=30°,
,得∠PBQ=∠CPA=30°,![]() ,进而得到∠BPC=60°,即可求解;
,进而得到∠BPC=60°,即可求解;
(2)以点C为坐标原点,BC所在直线为x轴,建立平面直角坐标系,如图2,
设点B(a,0),点P(x,0),根据坐标系中,中点坐标公式和两点间的距离公式,分别表示出MP,AP的长度,即可.
如图1,若![]() ,当
,当![]() 时,n=60°,理由如下:
时,n=60°,理由如下:
∵![]() 是等边三角形,
是等边三角形,
∴∠BAC=∠ACB=60°,
∵![]() ,
,
∴∠CAP=∠CPA=30°,
∵![]()
∴∠PBQ=∠CPA=30°,
∵![]() ,
,
∴![]() ,
,
∴∠Q=90°,
∴∠BPC=180°-∠Q -∠PBQ =180°-90°-30°= 60°,
∴n=60°;
(2)当n=120°时,对于![]() 延长线上任意一点P,总有
延长线上任意一点P,总有![]() ,理由如下:
,理由如下:
以点C为坐标原点,BC所在直线为x轴,建立平面直角坐标系,如图2,
设点B(a,0),点P(x,0),
∴PQ=PC=x,
∵∠CPQ=120°,
∴∠NPQ=180°-120°=60°,
过点Q作QH⊥x轴,则PH=![]() x,QH=
x,QH=![]() x,
x,
∴点Q坐标为(![]() ,
,![]() ),
),
∵点M时BQ的中点,
∴点M的坐标为:![]()
过点A作AE⊥x轴,则CE=![]() CB,AE=
CB,AE=![]() CE,
CE,
∴点A坐标为:![]() ,
,
∴AP=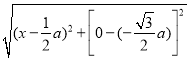 =
=![]()
MP=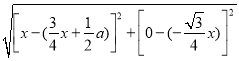 =
=![]() ,
,
即:![]() .
.
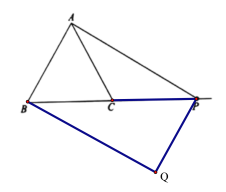
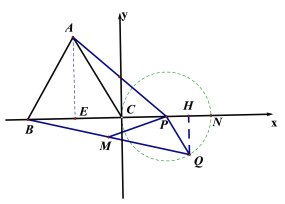
图1 图2


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】用适当的 方法解下列一元二次方程:
(1)(2x﹣1)2﹣9=0
(2)(x﹣1)(x+2)=4
(3)3x2﹣1=2x
(4)3(x﹣5)2=2(5﹣x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 于点
于点![]() ,连
,连![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ..其中正确结论的个数为( )
..其中正确结论的个数为( )

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
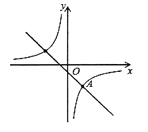
(1)求反比例函数的解析式;
(2)若一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,请直接写出关于x的不等式
,请直接写出关于x的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象经过点
的图象经过点![]() ,且当
,且当![]() 和
和![]() 时所对应的函数值相等.一次函数
时所对应的函数值相等.一次函数![]() 与二次函数
与二次函数![]() 的图象分别交于
的图象分别交于![]() ,
, ![]() 两点,点
两点,点![]() 在第一象限.
在第一象限.

(![]() )求二次函数
)求二次函数![]() 的表达式.
的表达式.
(![]() )连接
)连接![]() ,求
,求![]() 的长.
的长.
(![]() )连接
)连接![]() ,
, ![]() 是线段
是线段![]() 得中点,将点
得中点,将点![]() 绕点
绕点![]() 旋转
旋转![]() 得到点
得到点![]() ,连接
,连接![]() ,
, ![]() ,判断四边形
,判断四边形![]() 的性状,并证明你的结论.
的性状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “六一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
类别 | 儿童玩具 | 童车 | 童装 |
抽查件数 | 90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转![]() 得到线段PE,连接AE,BP,CE.
得到线段PE,连接AE,BP,CE.
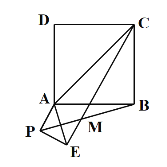
(1)求证:![]() ;
;
(2)当线段BP与CE相交时,设交点为M,求![]() 的值以及
的值以及![]() 的度数;
的度数;
(3)若正方形ABCD的边长为3,![]() ,当点P,C,E在同一直线上时,求线段BP的长.
,当点P,C,E在同一直线上时,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
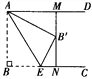
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com