
����Ŀ����ͼ��ʾ����֪������y��x2��bx��c��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C(0��-3)���Գ�����ֱ��x��1��ֱ��BC�������ߵĶԳ��ύ�ڵ�D��
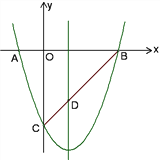
��1���������ߵĺ�������ʽ��
��2����ֱ��BC�ĺ�������ʽ��
��3����EΪy����һ���㣬CE�Ĵ�ֱƽ���߽�CE�ڵ�F������������P��Q���㣬�ҵ�P�ڵ������ޣ�
�ٵ��߶�PQ ![]() ʱ����tan��CED��ֵ��
ʱ����tan��CED��ֵ��
�ڵ���C��D��EΪ�������������ֱ��������ʱ����ֱ��д����P�����꣮
���ο���ʽ��������![]() �Ķ���������
�Ķ��������� ��
��
���𰸡���1�������ߵĺ�������ʽΪ![]() ����2��ֱ��BC�ĺ�������ʽΪ
����2��ֱ��BC�ĺ�������ʽΪ![]() ����3����
����3����![]() ��
��![]() ��
��  ��
��
�������������������1�����������ߵĶԳ��᷽�̿ɼ����b=-2���ٰ�C��0��-3�����������߽���ʽ�ɵõ�c=-3�����������ߵĺ�������ʽΪy=x2-2x-3��
��2��������������x��Ľ�������õ�A��-1��0����B��3��0����Ȼ�����ô���ϵ�������ֱ��BC�ĺ�������ʽ��
��3������AB=4��PQ=![]() AB=3�����������ߵĶԳ��Եõ�P���Q�����ֱ��x=1�Գƣ���P��-
AB=3�����������ߵĶԳ��Եõ�P���Q�����ֱ��x=1�Գƣ���P��-![]() ��-
��-![]() ��������F��0��-
��������F��0��-![]() ������FC=3-OF=
������FC=3-OF=![]() ������PQ��ֱƽ��CE�ڵ�F����CE=2FC=
������PQ��ֱƽ��CE�ڵ�F����CE=2FC=![]() ����D��1��-2��������D��DG��CE�ڵ�G����ͼ1����DG=1��CG=1������GE=CE=CG=
����D��1��-2��������D��DG��CE�ڵ�G����ͼ1����DG=1��CG=1������GE=CE=CG=![]() ��Ȼ����Rt��EGD�У��������еĶ�����⣻
��Ȼ����Rt��EGD�У��������еĶ�����⣻
����E��0��t�������������ľ��빫ʽ�õ�DE2=12+��t+2��2��CD2=12+��-2+3��2=2��EC2=��t+3��2��Ȼ��������ۣ�����CDE=90��ʱ��DE2+CD2=EC2����12+��t+2��2+2=��t+3��2������CED=90��ʱ��DE2+CE2=CD2����12+��t+2��2+��t+3��2=2������ECD=90��ʱ��CD2+CE2=DE2����2+��t+3��2=12+��t+2��2���ٷֱ�ⷽ�����tȷ��E�����꣬Ȼ����ݶ��κ���ͼ���ϵ����������ȷ��P�����꣮
���������
��1��������� �� ���
�� ���![]() ��
��
���������ߵĺ�������ʽΪ![]() ��
��
��2����![]() =0����
=0����![]() ��
��
����A(-1��0)��B(3��0)��
��ֱ��BC�ĺ�������ʽΪ![]() ��
��
�����B(3��0)�͵�C(0��-3)����![]()
���![]() ��
��
����ֱ��BC�ĺ�������ʽΪ![]() ��
��
��3������ͼ2��ʾ����ΪAB��4������PQ![]() ����ΪP��Q����ֱ��x��1�Գƣ�
����ΪP��Q����ֱ��x��1�Գƣ�
���Ե�P�ĺ�����Ϊ![]() �� ���Ե�P������Ϊ
�� ���Ե�P������Ϊ![]() ����F������Ϊ
����F������Ϊ![]() ��
��
���� ![]() ��
�� ![]() ��
��
���� ![]() ����E������Ϊ
����E������Ϊ![]() ��
��
ֱ��BC: ![]() �������ߵĶԳ���x��1�Ľ���D������Ϊ��1����2����
�������ߵĶԳ���x��1�Ľ���D������Ϊ��1����2����
����D��DH��y�ᣬ����ΪH�� ��Rt��EDH�У�DH��1�� ![]() ��
��
����tan��CED ��
��
����ͼ3��ͼ4�õ�P������Ϊ ![]() ��
��  ��
��

ͼ2 ͼ3 ͼ4
�㾦:�����Ƕ��κ������ۺ�����,�����漰����֪ʶ���������ߵĶ��㹫ʽ�������ε�������Լ��ô���ϵ������һ�κ����Ľ���ʽ�͵���ֱ�������ε�����,�����йض�������ʱҪע����������������۽��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������:��ͼ1,Բ�ĸ���:��ƽ����,�߶�PA�����̶���һ���˵�P��תһ��,��һ���˵�A���γɵ�ͼ�ν���Բ.����˵,��ij��������ڶ��������е���ͬһ��Բ��.Բ����P(a,b),�뾶Ϊr��Բ�ķ��̿���дΪ:(x-a)2+(y-b)2=r2.��:Բ����P(2,-1),�뾶Ϊ5��Բ�ķ���Ϊ:(x-2)2+(y+1)2=25.
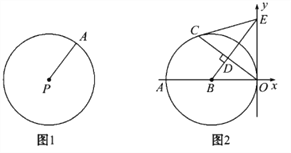
(1)���: ����A(3,0)ΪԲ��,1Ϊ�뾶��Բ�ķ���Ϊ:________; ����B(-1,-2)ΪԲ��, ![]() Ϊ�뾶��Բ�ķ���Ϊ:________;
Ϊ�뾶��Բ�ķ���Ϊ:________;
(2)�������ϲ��Ͻ����������:
��ͼ2,��B(-6,0)ΪԲ�ĵ�Բ��y��������ԭ��,C�Ǩ�B��һ��,����OC,��BD��OC����ΪD,�ӳ�BD��y���ڵ�E,��֪sin��AOC=![]() .
.
������EC,֤��EC�Ǩ�B������;
����BE���Ƿ����һ��P,ʹPB=PC=PE=PO,������,��P������,��д����PΪԲ��,��PBΪ�뾶�Ĩ�P�ķ���;��������,˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD������ECGF�ı߳��ֱ�Ϊ4��6����A=120�㣬����Ӱ���ֵ������ �� 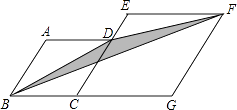
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѽ��ҹ������ºͳ��±��Ĵ�ͳ��Ӣ��ѧУ��ѧ��ȤС��Ϊ���˽ⱾУѧ��ϲ���±�������������ȡ��60��ͬѧ�����ʾ����飬����ͳ�ƺ�����������в�������ͳ��ͼ����ע�������ʾ������ÿһλͬѧ���κ�һ�ַ���ͳ����ֻ��һ��ѡ�������ͳ��ͼ����������⣺
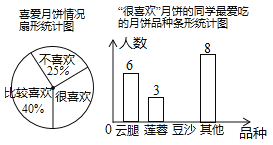
��1������ͳ��ͼ�У�����ϲ�����IJ�������Ӧ��Բ�Ľ�Ϊ�����ȣ�����ͳ��ͼ�У�����ϲ�����±���ϲ������ɳ���±���ѧ���������ˣ�
��2������У����ѧ��1200�ˣ���������������������Ƹ�Уѧ���С���ϲ�����±����������ˣ�
��3������ͬѧ��������±�������ͬѧ��Զ�ɳ�±���������������װ��ȫһ���Ķ�ɳ�����ء�����
�����±���һ������������ÿ�˸�ѡһ���������������˶�ѡ���Լ���Ե��±��ĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
��a2b+��3ab2��a2b����2��2ab2��a2b��������a��b����|a+1|+��b+2��2=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����OAB�У�OA=OB=10����AOB=80�㣬�Ե�OΪԲ�ģ�6Ϊ�뾶���Ż�![]() �ֱ�OA��OB�ڵ�M��N.
�ֱ�OA��OB�ڵ�M��N.
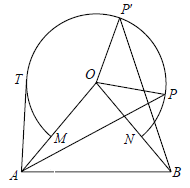
��1����P���Ұ뻡�ϣ���BOP����ǣ�����OP�Ƶ�O��ʱ����ת80���OP��. ��֤��AP = BP�䣻
��2����T����뻡�ϣ���AT�뻡![]() �����ڵ�T�����T��OA�ľ��룻
�����ڵ�T�����T��OA�ľ��룻
��3�����Q���Ż�![]() �ϣ�����AOQ��������ʱ��ֱ��д����BOQ�Ķ���.
�ϣ�����AOQ��������ʱ��ֱ��д����BOQ�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ε������߳��ֱ�Ϊ1��2��x����x��ȡֵ��Χ�ǣ� ��
A.1��x��3
B.1��x��3
C.1��x��3
D.1��x��3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com