当m=________时,二元二次六项式6x2+mxy-4y2-x+17y-15可以分解为两个关于x,y的二元一次三项式的乘积.
5或-
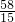
分析:本题先研究x,将x项和常数项进行十字分解,然后设出两个因式,相乘得到的结果与原多项式比较,可列出方程,从而达到结果,然后得到m的值.
解答:利用“十字相乘法”分解二次三项式的知识,可以判定给出的二元二次六项式
6x
2+mxy-4y
2-x+17y-15
中6x
2-x-15三项应当分解为:(3x-5)(2x+3);
现在要考虑y,只须先改写作(3x-5+ay)(2x+3+by);
然后根据-4y
2,17y这两项式,即可断定是:
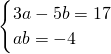
,
解得:a=4,b=-1,或a=

,b=-

.
又∵m=2a+3b,
∴当a=4,b=-1时,m=8-3=5;
当a=

,b=-

时,m=

-

=-
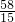
.
故答案为5或-
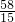
.
点评:本题考查十字相乘法分解因式,运用十字相乘法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程.

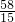
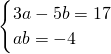 ,
, ,b=-
,b=- .
. ,b=-
,b=- 时,m=
时,m= -
- =-
=-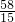 .
.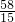 .
.
