
【题目】已知抛物线c1的顶点为A(﹣1,4),与y轴的交点为D(0,3).
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2,平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;
(4)若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)①4;②3;③3<n<4或n<3;(4)(﹣5,0)或(3﹣
;(3)①4;②3;③3<n<4或n<3;(4)(﹣5,0)或(3﹣![]() ,0)或(3+
,0)或(3+![]() ,0)或(﹣1,0).
,0)或(﹣1,0).
【解析】
试题分析:(1)设抛物线c1的解析式为![]() ,把D(0,3)代入
,把D(0,3)代入![]() 即可得到结论;
即可得到结论;
(2)解方程组得到![]() ,由于直线l1:y=x+m与c1仅有唯一的交点,于是得到△=9﹣4m+12=0,即可得到结论;
,由于直线l1:y=x+m与c1仅有唯一的交点,于是得到△=9﹣4m+12=0,即可得到结论;
(3)根据轴对称的性质得到抛物线c2的解析式为:![]() ,根据图象即可刚刚结论;
,根据图象即可刚刚结论;
(4)求得B(3,0),得到OB=3,根据勾股定理得到AB的长,①当AP=AB,②当AB=BP=![]() 时,③当AP=PB时,点P在AB的垂直平分线上,于是得到结论.
时,③当AP=PB时,点P在AB的垂直平分线上,于是得到结论.
试题解析:(1)∵抛物线c1的顶点为A(﹣1,4),∴设抛物线c1的解析式为![]() ,把D(0,3)代入
,把D(0,3)代入![]() 得3=a+4,∴a=﹣1,∴抛物线c1的解析式为:
得3=a+4,∴a=﹣1,∴抛物线c1的解析式为:![]() ,即
,即![]() ;
;
(2)解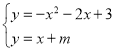 得
得![]() ,∵直线l1:y=x+m与c1仅有唯一的交点,∴△=9﹣4m+12=0,∴m=
,∵直线l1:y=x+m与c1仅有唯一的交点,∴△=9﹣4m+12=0,∴m=![]() ;
;
(3)∵抛物线c1关于y轴对称的抛物线记作c2,∴抛物线c2的顶点坐标为(1,4),与y轴的交点为(0,3),∴抛物线c2的解析式为:![]() ,∴①当直线l2过抛物线c1的顶点(﹣1,4)和抛物线记作c2的顶点(1,4)时,即n=4时,l2与c1和c2共有两个交点;
,∴①当直线l2过抛物线c1的顶点(﹣1,4)和抛物线记作c2的顶点(1,4)时,即n=4时,l2与c1和c2共有两个交点;
②当直线l2过D(0,3)时,即n=3时,l2与c1和c2共有三个交点;
③当3<n<4或n<3时,l2与c1和c2共有四个交点;
(4)如图,∵若c2与x轴正半轴交于B,∴B(3,0),∴OB=3,∴AB=![]() =
=![]() :
:
①当AP=AB=![]() 时,PB=8,∴P1(﹣5,0);
时,PB=8,∴P1(﹣5,0);
②当AB=BP=![]() 时,P2(3﹣
时,P2(3﹣![]() ,0)或P3(3+
,0)或P3(3+![]() ,0);
,0);
③当AP=PB时,点P在AB的垂直平分线上,∴PA=PB=4,∴P4(﹣1,0).
综上所述,点P的坐标为(﹣5,0)或(3﹣![]() ,0)或(3+
,0)或(3+![]() ,0)或(﹣1,0)时,△PAB为等腰三角形.
,0)或(﹣1,0)时,△PAB为等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, ![]() 为坐标原点,直线
为坐标原点,直线 ![]() :
: ![]() 与直线
与直线 ![]() :
: ![]() 交于点
交于点 ![]() ,
, ![]() 与
与 ![]() 轴交于
轴交于 ![]() ,与
,与 ![]() 轴交于点
轴交于点 ![]() .
.
(1)求 ![]() 的面积;
的面积;
(2)若点 ![]() 在直线
在直线 ![]() 上,且使得
上,且使得 ![]() 的面积是
的面积是 ![]() 面积的
面积的 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
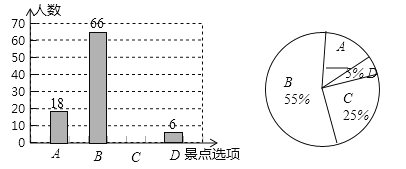
【题目】为了丰富同学们的课余生活,某学校计划举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生必须从“A(洪家关),B(天门山),C(大峡谷),D(黄龙洞)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
请你根据图中所提供的信息,完成下列问题:
(1)本次调查的学生人数为 ;
(2)在扇形统计图中,“天门山”部分所占圆心角的度数为 ;
(3)请将两个统计图补充完整;
(4)若该校共有2000名学生,估计该校最想去大峡谷的学生人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离(结果精确到0.1km).参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com