
 解不等式2(2x-3)<5(x-1),并把它的解集在数轴上表示出来.
解不等式2(2x-3)<5(x-1),并把它的解集在数轴上表示出来.  考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点A(-2,-4),直线x=-2与x轴相交于点B,连接OA,抛物线y=-x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到点A时停止移动.
如图,在平面直角坐标系中,已知点A(-2,-4),直线x=-2与x轴相交于点B,连接OA,抛物线y=-x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到点A时停止移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
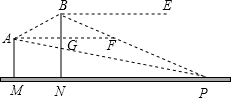 某直升飞机在我方追击炮阵地M上方测得敌军雷达站P的俯角为15°,在向点P的迎面沿仰角30°的方向飞行,升高100米后再测点P的俯角为30°,分别求原飞行高度和点M到点P的水平距离(tan15°=2-$\sqrt{3}$,cot15°=2+$\sqrt{3}$)
某直升飞机在我方追击炮阵地M上方测得敌军雷达站P的俯角为15°,在向点P的迎面沿仰角30°的方向飞行,升高100米后再测点P的俯角为30°,分别求原飞行高度和点M到点P的水平距离(tan15°=2-$\sqrt{3}$,cot15°=2+$\sqrt{3}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com