
【题目】在平面直角坐标系中画出两条相交直线y=x和y=kx+b,交点为(x0 , y0),在x轴上表示出不与x0重合的x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后在x轴上确定对应的数x2 , …,依次类推到(xn , yn-1),我们来研究随着n的不断增加,xn的变化情况.如图1(注意:图在下页上),若k=2,b=—4,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;如图2,若k= ![]() ,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 .
,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 . 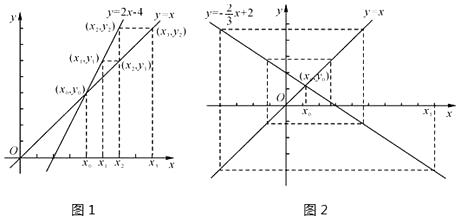
【答案】远离;靠近;-1<k<1且k≠0
【解析】(1)由分析可知第1空填“远离”,(2)第2空填“靠近”;
(3)联立方程组![]() 解得
解得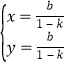
即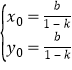 .
.
I.当k>1时,y=kx+b随着x的增大而增大,
则x>x0时kx+b>x
取x1>x0 , 则kx1+b>x1,即y1=kx1+b>x1;
由题意得x2=y1=kx1+b>x1,
同理,x3=y2=kx2+b>x2,
……
xn=yn-1=kxn-1+b>xn-1,
所以得到一组点(x1,y1),(x2,y1),(x2,y2),…,(xn,yn-1) ,
且x0<x1<x2<x3<…<xn,
则k>1时,随着n的不断增加,xn逐渐远离x0;
同理可得,当k<-1时,随着n的不断增加,xn逐渐远离x0
II.当0<k<1时,y=kx+b随着x的增大而增大,
则x>x0时kx+b<x
取x1>x0 , 则x0<kx1+b<x1,即x0=y0<y1=kx1+b<x1;
由题意得x2=y1=kx1+b,则x0<x2<x1,
同理,x3=y2=kx2+b<x2,则x0<x3<x2,
……
xn=yn-1=kxn-1+b<xn-1,则x0<xn<xn-1,
所以得到一组点(x1,y1),(x2,y1),(x2,y2),…,(xn,yn-1) ,
且x0<xn<xn-1<…<x3<x2<x1,
则0<k<1时,随着n的不断增加,xn逐渐靠近x0;
同理可得,当-1<k<0时,随着n的不断增加,xn逐渐靠近x0.
综上-1<k<1且k≠0时,随着n的不断增加,xn逐渐靠近x0.
故答案为-1<k<1且k≠0.
根据图1和图2,观察(xn , yn-1)的位置,
(1)容易看到图1中的(xn , yn-1)与(x0 , y0)越来越远;
(2)容易看到图2中的(xn , yn-1)与(x0 , y0)越来越靠近;
(3)根据图1和图2的例子,可以分k>1,k<-1,0<k<1和-1<k<0分类讨论,求出xn的值变化情况即可.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2.
﹣2.
请解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知:x是3+![]() 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC﹣BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=4AD,其中正确的有( )
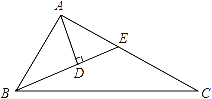
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
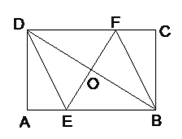
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题: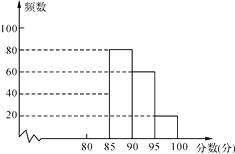
分数段 | 频数 | 频率 |
80≤x<85 | a | 0.2 |
85≤x<90 | 80 | b |
90≤x<95 | 60 | c |
95≤x<100 | 20 | 0.1 |
(1)求出表中a,b,c的数值,并补全频数分布直方图;
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
.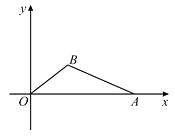
(1)在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹)
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿 ![]() 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个转盘,转盘被分成4个相同的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率:
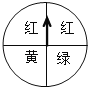
(1)指针指向绿色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com