
����Ŀ����ͼ����֪������y��ax2��bx��c��a��0���ĶԳ���Ϊֱ��x����1���Ҿ���A��1��0����C��0��3�����㣬��x�����һ������ΪB.
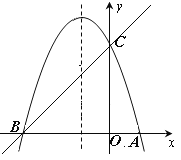
��1����ֱ��y��mx��n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
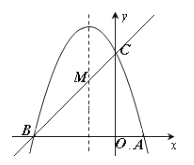
��2���������ߵĶԳ���x����1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�����M�����ꣻ��3�����PΪ�����ߵĶԳ���x����1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
���𰸡���1��![]() ��
��![]() ����2��M����1��2������3�����������ĵ�P�����ĸ�,�ֱ�Ϊ
����2��M����1��2������3�����������ĵ�P�����ĸ�,�ֱ�Ϊ![]() ����1����2��,
����1����2��, ![]() ����1��4��,
����1��4��, ![]() ����1��
����1��![]() �� ,
�� ,![]() ����1��
����1��![]() ����
����
��������
�����������1����֪������y��ax2��bx��c�ĶԳ���Ϊֱ��x����1���Ҿ���A��1��0����C��0��3�����㣬�ɵ÷����飬�ⷽ��������a��b��c��ֵ�����ɵ������ߵĽ���ʽ�����������ߵĶԳ��Ժ͵�A��������1��0�������B�����������3��0�����ô���ϵ���������ֱ��BC�Ľ���ʽ����2��ʹMA+MC��С�ĵ�MӦΪֱ��BC��Գ���x����1�Ľ��㣬��x=-1����ֱ��BC�Ľ���ʽ���y��ֵ�����ɵõ�M�����ꣻ��3������BΪֱ�Ƕ��㣬��CΪֱ�Ƕ��㣬��PΪֱ�Ƕ�����������ֱ����P�����꣮
�����������1�������⣬��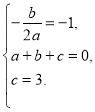 ��֮����
��֮����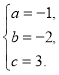
�������߽���ʽΪ![]() ��
��
���Գ���Ϊx����1���������߾���A��1��0����
��B����3��0����
��B����3��0����C��0��3���ֱ�ֱ��y��mx��n����
![]() ��֮����
��֮����![]()
��ֱ��BC�Ľ���ʽΪ![]() ��
��
��2����MA=MB����MA+MC=MB+MC.
��ʹMA+MC��С�ĵ�MӦΪֱ��BC��Գ���x����1�Ľ���.
��ֱ��BC��Գ���x����1�Ľ���ΪM����x����1
����ֱ��![]() ����y��2.
����y��2.
��M����1��2��
��3����P����1��t�������B����3��0����C��0�� 3������BC2��18��
PB2������1��3��2��t2��4��t2��
PC2������1��2����t��3��2��t2��6t��10.
����BΪֱ�Ƕ��㣬��BC2��PB2��PC2����18��4��t2��t2��6t��10.
��֮,��t����2.
����CΪֱ�Ƕ��㣬��BC2��PC2��PB2����
18��t2��6t��10��4��t2����֮����t��4��
����PΪֱ�Ƕ��㣬��PB2��PC2��BC2����
4��t2��t2��6t��10��18����֮����t1��![]() ��t2��
��t2��![]() ��
��
�������������������ĵ�P�����ĸ�,�ֱ�Ϊ![]() ����1����2��,
����1����2��, ![]() ����1��4��,
����1��4��, ![]() ����1��
����1��![]() �� ,
�� ,![]() ����1��
����1��![]() ����
����


 �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��x��y�����ֽ�������ƽ��5����λ��������ƽ��4����λ���õ���P������2y����2x����
��1��Ϊ����õ�P�͵�P�������꣬����������з�����Ϊ ��
��2������ͼ����������飻
��3����д����P�͵�P�������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A. �����ȱ�������ȫ��
B. ����һ������40�����������������ȫ��
C. �Խ����ഹֱƽ�ֵ��ı���������
D. �ԽǷ����ഹֱ����ȵ��ı�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=ax2+bx+c�Ķ�����A��2����1�����Ҿ�����B��1��0�����������ߵĺ�����ϵʽΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A. x4x4=x16 B. ��a3��2a4=a9
C. ��ab2��3�£���ab��2=��ab4 D. ��a6��2�£�a4��3=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г��ȵ������߶�����������ε��ǣ�������
A. 2��3��5 B. 7��4��2 C. 3��4��8 D. 3��3��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������һ�����Ϊ400ƽ������������ֽƬ�����űߵķ���ó�һ�����Ϊ300ƽ�����ij�����ֽƬ��ʹ���ij���֮��Ϊ3��2����֪�ܷ�ó��������ڷ��С������˵�����һ������һ��������ֽƬ�ó�һ�����С��ֽƬ������ͬ��С����˵������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����Ϊ1����һ�β������ֱ��ӳ�AB,BC,CA����A1,B1,C1,ʹA1B=AB,B1C=BC,C1A=CA,˳������A1,B1,C1,�õ���A1B1C1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1����A2��B2��C2��ʹA2B1=A1B1��B2C1=B1C1��C2A1=C1A1��˳������A2��B2��C2���õ���A2B2C2�������˹��ɣ�Ҫʹ�õ��������ε��������2010�����پ������β��� ���� ����
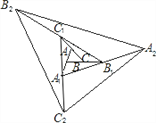
A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com