
【题目】如图,在四边形ABCD中,AB=BC=2,CD=3,DA=1,且AB⊥BC于B.
求:(1)∠BAD的度数;
(2)四边形ABCD的面积.

【答案】(1)∠BAD=135°;(2)四边形ABCD的面积为2+![]() .
.
【解析】
(1)由于∠B=90°,AB=BC=2,利用勾股定理可求AC,并可求∠BAC=45°,而CD=3,DA=1,易得AC2+DA2=CD2,可证△ACD是直角三角形,∠CAD=90°,从而易求∠BAD的度数;
(2)由三角形的面积公式即可得出结果.
(1)连接AC,

∵∠B=90°,AB=BC=2,
∴AC=![]() =2
=2![]() ,∠BAC=45°,
,∠BAC=45°,
又∵CD=3,DA=1,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠BAD=45°+90°=135°;
(2)四边形ABCD的面积=△ABC的面积+△ACD的面积=![]() ×2×2+
×2×2+![]() ×1×2
×1×2![]() =2+
=2+![]()


科目:初中数学 来源: 题型:
【题目】某校对全校3000名学生本学期参加艺术学习活动的情况进行评价,其中甲班学生本学期参观美术馆的次数以及艺术评价等级和艺术赋分的统计情况,如下表所示:

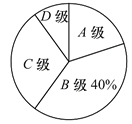
图(1) 图(2)
(1)甲班学生总数为______________人,表格中![]() 的值为_____________;
的值为_____________;
(2)甲班学生艺术赋分的平均分是______________分;
(3)根据统计结果,估计全校3000名学生艺术评价等级为![]() 级的人数是多少?
级的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
![]() 若
若![]() ,
,![]() ,且二次函数的图象经过点
,且二次函数的图象经过点![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() ,
,![]() ,
,![]() ,且二次函数的图象经过点
,且二次函数的图象经过点![]() ,求证:
,求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,且二次函数的图象经过点
,且二次函数的图象经过点![]() ,试问当自变量
,试问当自变量![]() 时,二次函数
时,二次函数![]() 所对应的函数值
所对应的函数值![]() 是否大于
是否大于![]() ?请证明你的结论.
?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将线段![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]() 得到线段
得到线段![]() ,连接
,连接![]() 得
得![]() ,又将线段
,又将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() (如图①).
(如图①).
![]() 求
求![]() 的大小(结果用含
的大小(结果用含![]() 的式子表示);
的式子表示);
![]() 又将线段
又将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得线段
得线段![]() ,连接
,连接![]() (如图②)求
(如图②)求![]() ;
;
![]() 连接
连接![]() 、
、![]() ,试探究当
,试探究当![]() 为何值时,
为何值时,![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是关于x的一次函数,下表列出了这个函数部分的对应值:

(1)求这个一次函数的表达式.
(2)求m,n的值.
(3)已知点![]() 和点
和点![]() 在该一次函数图象上,设
在该一次函数图象上,设![]() ,判断正比例函数
,判断正比例函数![]() 的图象是否有可能经过第一象限,并说明理由.
的图象是否有可能经过第一象限,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幢建筑物,从10米高的窗口A用水管和向外喷水,喷的水流呈抛物线(抛物线所在平面与墙面垂直),(如图)如果抛物线的最高点M离墙1米,离地面![]() 米,则水流下落点B离墙距离OB是( )
米,则水流下落点B离墙距离OB是( )

A. 2米 B. 3米 C. 4米 D. 5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
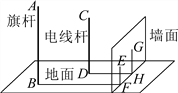
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com