
 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交与点O,AD与BC交与点P,BE与CD交与点Q,连接PQ.有下列结论:
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交与点O,AD与BC交与点P,BE与CD交与点Q,连接PQ.有下列结论:| A. | ①②③⑤ | B. | ①③④⑤ | C. | ①②⑤ | D. | ②③④ |
分析 根据等边三角形性质得出AC=BC,DC=CE,∠BCA=∠DCE=60°,求出∠ACD=∠BCE,证△ACD≌△BCE,推出AD=BE,即可判断①;根据全等三角形性质得出∠CBE=∠CAD,根据ASA证△ACP≌△BCQ,推出AP=BQ,即可判断②;对应角相等可得∠CAD=∠CBE,然后证明△ACP与△BCQ全等,根据全等三角形对应角相等可得PC=PQ,从而得到△CPQ是等边三角形,所以⑤正确求出∠DCE=60°=∠CAD+∠ADC,求出∠CAD+∠BEC=60°,即可求出∠AOB=60°,即可判断③;根据三角形外角性质推出∠DPC>∠DCP,推出DP<DC,即可判断④.
解答 解:∵△ABC和△DCE是正三角形,
∴AC=BC,DC=CE,∠BCA=∠DCE=60°,
∴∠BCA+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=CE}\end{array}\right.$
∴△ACD≌△BCE(SAS),
∴AD=BE,∴①正确;
∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∵∠ACB=∠DCE=60°,
∴∠BCD=60°=∠ACB,
在△ACP和△BCQ中$\left\{\begin{array}{l}{∠CAP=∠CBQ}\\{AC=BC}\\{∠ACP=∠BCQ}\end{array}\right.$
∴△ACP≌△BCQ(ASA),
∴AP=BQ,∴②正确;
PC=QC,
∴△CPQ为正三角形∴⑤正确
∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∠DCE=60°=∠CAD+∠ADC,
∴∠CAD+∠BEC=60°,
∴∠AOB=∠CAD+∠BEC=60°,∴③正确;
∵△DCE是正三角形,
∴DE=DC,
∵∠AOB=60°,∠DCP=60°,∠DPC>∠AOB,
∴∠DPC>∠DCP,
∴DP<DC,即DP<DE,∴④错误;
所以正确的有①②③⑤,
故选A.
点评 本题考查了等边三角形性质,全等三角形的性质和判定,三角形的外角性质,主要考查学生综合运用性质进行推理的能力,本题综合性比较强,有一定的难度


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
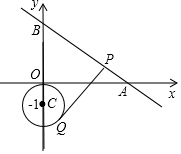 如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点A、B;点Q是以C(0,-2)为圆心、2为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是2$\sqrt{3}$.
如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点A、B;点Q是以C(0,-2)为圆心、2为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com