Question

11．已知抛物线y=x²上有两动点A（x₁，y₁），B（x₂，y₂），其中0＜x₁＜x₂），过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，OA的延长线交BD于点E．
（1）如图1，若点A的坐标为（1，1），点B的坐标为（2，4），则点E的坐标为（2，2）．
（2）如图2，过A作AF⊥BD于F．若BE=AE，试求BF的长；
（3）如图3，延长CA交OB于点H．若S_△OEH=$\frac{1}{3}$S_{四边形OHED}，试探究x₁和x₂之间的数量关系，并证明你的结论．

Answer 1

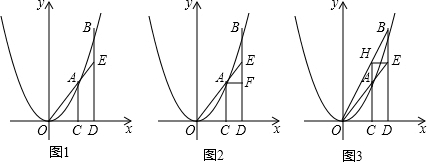
分析 （1）如图1中，求出直线OA的解析式，根据点B坐标即可求出点E坐标．
（2）如图2中，根据AE=BE，列出关于y₁，y₂的方程，求出y₂-y₁即可解决问题．
（3）如图3中，先证明四边形HCDE是矩形，再证明S_△HOC=S_△HCD=S_△HDE即可解决问题．

解答 解：（1）如图1中，∵点A坐标（1，1），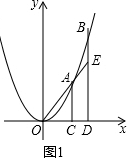
∴直线OA解析式为y=x，
∵点B坐标（2，4），
∴点E坐标（2，2）．
故答案为（2，2）．
（2）如图2中，∵点A（x₁，y₁），
∴直线OA解析式y=$\frac{{y}_{1}}{{x}_{1}}$x，
∵点B坐标（x₂，y₂），
∴点E坐标（x₂，$\frac{{x}_{2}{y}_{1}}{{x}_{1}}$），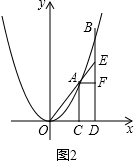
∵AE=EB，
∴$\sqrt{（{x}_{1}-{x}_{2}）^{2}+（\frac{{x}_{2}{y}_{1}}{{x}_{1}}-{y}_{1}）^{2}}$=y₂-$\frac{{x}_{2}{y}_{1}}{{x}_{1}}$，
∴（x₂-x₁）$•\sqrt{1+\frac{{{y}^{2}}_{1}}{{{x}_{1}}^{2}}}$=y₂-$\frac{{x}_{2}{y}_{1}}{{x}_{1}}$，
∵y₁=x₁²，y₂=x₂²，
∴x₁=$\sqrt{{y}_{1}}$，x₂=$\sqrt{{y}_{2}}$，
∴（$\sqrt{{y}_{2}}$-$\sqrt{{y}_{1}}$）•$\sqrt{1+{y}_{1}}$=$\sqrt{{y}_{2}}$（$\sqrt{{y}_{2}}$-$\sqrt{{y}_{1}}$），
∴$\sqrt{1+{y}_{1}}$=$\sqrt{{y}_{2}}$，
∴1+y₁=y₂，
∴y₂-y₁=1，
∴BF=y₂-y₁=1．
（3）结论x₂=2x₁．
理由：如图3中，∵点A（x₁，y₁），B（x₂，y₂），
∴直线OA解析式为y=$\frac{{y}_{1}}{{x}_{1}}$x，直线OB解析式为y=$\frac{{y}_{2}}{{x}_{2}}$x，
∴点H坐标（x₁，$\frac{{y}_{2}{x}_{1}}{{x}_{2}}$），点E坐标（x₂，$\frac{{y}_{1}{x}_{2}}{{x}_{1}}$），
∵y₂=x₂²，y₁=x₁²，
∴$\frac{{y}_{2}{x}_{1}}{{x}_{2}}$=x₁x₂，$\frac{{y}_{1}{x}_{2}}{{x}_{1}}$=x₁x₂，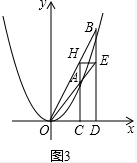
∴HC=ED，
∵HC∥ED，
∴四边形HCDE是平行四边形，∵∠HCD=90°，
∴四边形HCDE是矩形，
∴HE∥OD，
∴S_△HOE=S_△HED=S_△HCD，
∵S_△OEH=$\frac{1}{3}$S_{四边形OHED}，
∴S_△HOC=S_△HCD=S_△HDE，
∴OC=CD，
∴x₂=2x₁．

点评 本题考查二次函数综合题、一次函数、两点间距离公式、平行线的性质等知识，解题的关键是学会利用参数解决问题，本题目有一定的代数运算技巧，解题的突破口是发现HE∥OD，属于中考压轴题．