
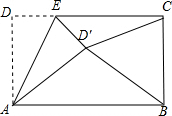
 如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中:
如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 当D′落在线段AB上时,D′B的值最小,此时D′B=AB-AD=3,得出①正确;当点A、D′、C在同一直线上,则CD′的最小值,由此求出AC的长度,得出②正确;过D′作MN⊥AB交AB于点N,交CD于点M,设AN=x,则EM=x-2.5,证出∠ED′M=∠D′AN,因此△EMD′∽△D′NA,得出对应边成比例$\frac{ED′}{AD′}$=$\frac{EM}{D′N}$,求出x=4,得出AN=BN,因此AD′=D′B,得出④正确;当DE=$8-\sqrt{39}$时,假设△ABD′是直角三角形,则E、D′、B在一条直线上,作EF⊥AB于点F,由勾股定理求出D′B、EB,得出③正确;
解答  解:当D′落在线段AB上时,D′B的值最小,如图1所示:
解:当D′落在线段AB上时,D′B的值最小,如图1所示:
此时D′B=AB-AD=8-5=3,
∴①正确;
如图2,当点A、D′、C在同一直线上时,CD′取最小值,
∵四边形ABCD为矩形,
∴∠D=90°,AD=5,CD=AB=8,
由勾股定理求得AC=$\sqrt{89}$;
∵点A、D′、C在同一直线上,
∴D′C=AC-AD′=AC-AD=$\sqrt{89}$-5,
∴②正确;
过D′作MN⊥AB交AB于点N,交CD于点M,如图3所示:
设AN=x,则EM=x-2.5,
∵∠AD′N=∠DAD′,∠ED′M=180°-∠AD′E-∠AD′N=180°-90°-∠AD′N=90°-∠AD′N,
∴∠ED′M=90°-∠DAD′,
∵∠D′AN=90°-∠DAD′,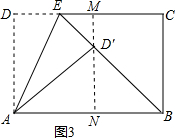
∴∠ED′M=∠D′AN,
∵MN⊥AB,
∴∠EMD′=∠AND′,
∴△EMD′∽△D′NA,
∴$\frac{ED′}{AD′}$=$\frac{EM}{D′N}$,
即$\frac{2.5}{5}$=$\frac{x-2.5}{\sqrt{{5}^{2}-{x}^{2}}}$,
解得:x=4,
∴AN=BN,
∴AD′=D′B,
即△ABD′是等腰三角形,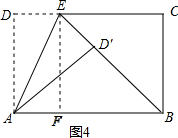
∴④正确;
当DE=$8-\sqrt{39}$时,假设△ABD′是直角三角形,
则E、D′、B在一条直线上,
作EF⊥AB于点F,如图4所示:
D′B=$\sqrt{A{B}^{2}-D′{A}^{2}}$=$\sqrt{{8}^{2}-{5}^{2}}$=$\sqrt{39}$,EB=$\sqrt{E{F}^{2}+F{B}^{2}}$=8,
∵8-$\sqrt{39}$+$\sqrt{39}$=8,
∴BD′+ED′=EB,
∴③正确.
故选D.
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理、等腰三角形的判定、勾股定理的逆定理、等腰直角三角形的判定等知识;本题综合性强,有一定难度,熟练掌握矩形的性质和翻折变换的性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$
在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
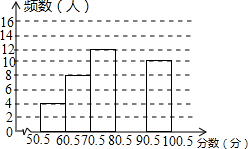 2015年11月9日是第25个全国消防日,某学校为了增强学生的安全意识,举行了一次安全知识竞赛,全校800名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中随机抽取了部分学生的成绩进行统计(满分100分,而且成绩均为整数).绘制了不完整的统计图表,请你根据图表中提供的信息解答以下问题:
2015年11月9日是第25个全国消防日,某学校为了增强学生的安全意识,举行了一次安全知识竞赛,全校800名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中随机抽取了部分学生的成绩进行统计(满分100分,而且成绩均为整数).绘制了不完整的统计图表,请你根据图表中提供的信息解答以下问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 12 | m |
| 80.5~90.5 | n | 0.32 |
| 90.5~100.5 | 10 | 0.1 |
| 合计 | a | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、B为x轴上的两点,点C、D为y轴上的两点,经过A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线成为“月线”.已知点C的坐标为(0,3),点M是抛物线C2:y=mx2-4mx-12m(m<0)的顶点.
如图,点A、B为x轴上的两点,点C、D为y轴上的两点,经过A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线成为“月线”.已知点C的坐标为(0,3),点M是抛物线C2:y=mx2-4mx-12m(m<0)的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在不透明的箱子里放有4个乒乓球.每个乒乓球上分别写有数字1、2、3、4,从箱子中摸出一个球记下数字后放回箱中,摇匀后再摸出一个球记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出的球上的数字记为点的纵坐标.
在不透明的箱子里放有4个乒乓球.每个乒乓球上分别写有数字1、2、3、4,从箱子中摸出一个球记下数字后放回箱中,摇匀后再摸出一个球记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出的球上的数字记为点的纵坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
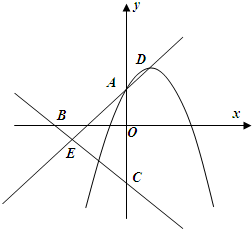 如图,抛物线y=-x2+2x+m(m>0)与y轴交于A,顶点为D,直线y=-$\frac{1}{2}$x-2m分别与x轴、y轴交于B、C两点,与直线AD相交于E点.
如图,抛物线y=-x2+2x+m(m>0)与y轴交于A,顶点为D,直线y=-$\frac{1}{2}$x-2m分别与x轴、y轴交于B、C两点,与直线AD相交于E点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com